Distributivgesetz
Für zwei unterschiedliche mathematische Operationen (°,) gilt das Distributivgesetz, wenn folgende Bedingung erfüllt ist:
A ° (B C) = (A ° B) (A ° C)
Wenn das Distributivgesetz auf die Operationen (°,) zutrifft, muss dies aber NICHT bedeuten, dass es auch für die Operationen (,°) gilt. Dies soll am Beispiel der Addition und Multiplikation in der Grundmenge der natürlichen Zahlen gezeigt werden:
Das Distributivgesetz gilt für (×,+):
2×(3+4)=(2×3)+(2×4)
Linke Seite: 2×(3+4)=2×7=14
Rechte Seite: (2×3)+(2×4)=6+8=14 -> Wahre Aussage
Für (+,×) gilt das Distributivgesetz nicht:
2+(3×4)=(2+3)×(2+4)
Linke Seite: 2+(3×4)=2+12=14
Rechte Seite: (2+3)×(2+4)=5×6=30 -> Falsche Aussage
Distributivgesetz für Mengenoperationen
Bei den Mengenoperationen gelten folgende Distributivgesetze zwischen
Schnittmenge und Vereinigung:
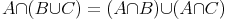
Vereinigung und Schnittmenge:
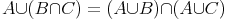
Schnittmenge und Differenz:
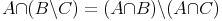
Es gilt jedoch nicht Differenz und Schnittmenge, Vereinigung und Differenz bzw. Differenz und Vereinigung
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar