Dezimalzahl in Binärzahl umwandeln
Um eine Dezimalzahl in eine Binärzahl umzuwandeln, muss die Dezimalzahl nur durch die Zahl 2 dividiert und der Rest notiert werden.
Da eine Zahl dividiert durch 2 immer nur den Rest 0 oder 1 ergeben kann (da beim Rest 2 der Quotient um 1 erhöht werden müsste), entsteht daraus die äquivalente Binärzahl. Folgende Schritte müssen immer wieder durchgeführt werden:
- Die Zahl durch 2 dividieren
- Den Rest der Division notieren
- Falls das Ergebnis nicht 0 ist, Schritt 1 und 2 wiederholen
Dezimalzahl in Binärzahl - Beispiel:
| Zahl | Quotient | Rest |
|---|---|---|
| 190:2= | 95 | 0 |
| 95:2= | 47 | 1 |
| 47:2= | 23 | 1 |
| 23:2= | 11 | 1 |
| 11:2= | 5 | 1 |
| 5:2= | 2 | 1 |
| 2:2= | 1 | 0 |
| 1:2= | 0 | 1 |
Die Dezimalzahl 190 ergibt daher die Binärzahl:
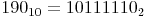
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Sandra Müller
ANGEBLICH, ich weiß es selber nicht ist diese Methode nur beschränkt möglich ,weil man bei bestimmten Zahlen oft sinnlos dividieren muss.
Claudia
Hallo,
warum liest man den Rest dann von unten nach oben?
LG
Mau
Liebe Sandra, wenn du entwas nicht weisst, wieso entschließt du dich dazu mit deiner Falschaussage andere Leute zu verunsichern? Der Algorithmus ist in sich schlüssig, klappt mit jeder Zahl.
Marko
Klar & verständlich formuliert. Danke !
obst
also mit 0,5 funktioniert das meiner meinung nach nicht
GrafZahl
Man kann nur zahlen bis 255 rechnen wenn man eine 8 stellige binär zahl haben will. Dies gilt aber nur wenn man ein byte in binär darstellen will, theoretisch geht dies mit jeder zahl.
Manu
Geschätzter Admin
Herzlichen Dank für das tolle System. In diesem Beispiel geht die Rechnung auf. Wenn ich das aber nachrechne, anhand einer anderen Zahl z.B. 95, dann verstehe ich dieses System nicht mehr. Kannst du ein weiteres Beispiel mit 95 machen und die Wiederholungsschritte genauer erläutern? Ansonsten echt super :) Herzlichen Dank, Manu
nikodemus
@obst 0,5 Dezimal geht auch, nur umgekehrt: man muss mit 2 Multiplizieren. Alles was links rausfaellt, sind die Nachkommastellen, Ergebnis daher: 0,1 Binaer
peter karl heins
diese seite hat mir aus einem informatiktest geholfen, danke
samol
ist zwar schon etwas her, aber ich hoffe irgendjemand liest das und kann mir helfen: Warum ergibt hier 1:2=0 ?? (und nicht 0,5)
Lars
Hallo samol,
1:2=0 weil du bei dieser Methode immer mit Rest teilst. da 1<2 ist 1:2=0 mit Rest 1.
Pete
Danke
Kai meilicke
sehr hilfreich
jeyjo
klapt das mit allen Zahlen?
danke
DontCare
was geschieht mit den Zahlen über 255 ? gibt es dabei einen Trick ?
@ jeyjo: nur mit Zahlen unter 255
Max Sittig
Danke mir hat das weiter geholfen :^)
derhauer
Geiles ding
Shnyxz
Danke, endlich verstanden was der Lehrer in 4 Stunden nicht erklären konnte
lululemin
ICH HABE NICHTS VERSTANDEN BITTE ÄNDERN SIE DIES
@lululermin
LOL XD was gibts da nd zu verstegen
manuel
gut erklärt
Matze
So genial erklärt und trotzdem verstehen es Einige nicht. Das Ergebnis ist jeweils auf natürliche Zahlen zu begrenzen, deshalb gibt es ja einen Rest. Das ist 1. Klasse. Und da gibt es eben 0,5 nicht, daher ist 1:2 = 0 Rest 1
Geht auch mit größeren Zahlen, entsprechend mehr Stellen hat eben die Binärzahl....
Nils
Durch 2 dividiert heiß doch geteilt durch 2 ?
Felix
Und wie geht das mit 192? Da hat am Ende einen Rest von 2!
Sebastian
lieber Felix, nein, ich hoffe du bist kein Troll...
Binär ist die Basis 2 ( 2 Zustände ). Binär unterscheidet immer nur 2 mögliche Zustände. 1 und 0... es gibt keine 2,3,4,5,6,7,8 oder 9.
In der Umrechnung zu Binär, rechnen wir immer mit der vollen Dezimalzahl. Das bedeutet z.B. das wir bei 3 / 2 = 1,5 , nur mit 1 ( anstatt 1,5 ) weiter rechnen, aber sieh selbst :
192 / 2 = 96 Rest 0 <- LSB *
96 / 2 = 48 Rest 0
48 / 2 = 24 Rest 0
24 / 2 = 12 Rest 0
12 / 2 = 6 Rest 0
6 / 2 = 3 Rest 0
der nächste Schritt wäre nun :
( 3 / 2 = 1,5 ) ( 2 x 1 + 2 x 0,5 = 3)
da wir aber im binär nur ganze Dezimalzahlen verwenden dürfen lautet die nächste Zeile :
3 / 2 = 1 Rest 1
( 1 x 2 = 2, 3 - 2 = "1" )
1 / 2 = 0 Rest 1 <- MSB *
( 0 x 2 = 0 )
*LSB = Last significant Bit
*MSB = Most significant Bit
Der Binärcode für 192 wird nun vom MSB zum LSB abgelesen und zum besseren Verständniss nach 4 Ziffern wie folgt notiert :
1100 0000,
11000000, ist trotzdem korrekt ! Nur schwerer zu lesen.
Die 9te Stelle ist überflüssig, da nach der 8ten Stelle die Division ( das teilen ) auf 0 abgeschlossen ist. Damit wird die 9te Stelle nicht mehr berücksichtigt.
Anders ist das z.B. bei 1500
1500 / 2 = 750 Rest 0 <- LSB
750 / 2 = 375 Rest 0
375 / 2 = 187 Rest 1
(2 x 187 = 374, 375 - 374 = "1" )
187 / 2 = 93 Rest 1
(2 x 93 = 186, 187 - 186 = "1" )
93 / 2 = 46 Rest 1
46 / 2 = 23 Rest 0
23 / 2 = 11 Rest 1
11 / 2 = 5 Rest 1
5 / 2 = 2 Rest 1
2 / 2 = 1 Rest 0
1 / 2 = 0 Rest 1 <- MSB
0 / 2 = 0 Rest 0 (<- nicht berücksichtigt )
Der Binärcode für 1500 lautet also :
101 1101 1100
Dieser Rechenweg funktioniert bis zu einer Zahl von 4294967295, aber warum das so ist kann ich nicht mehr erklären.
Sebastian
192 / 2 = 96 Rest 0 <- LSB *
96 / 2 = 48 Rest 0
48 / 2 = 24 Rest 0
24 / 2 = 12 Rest 0
12 / 2 = 6 Rest 0
6 / 2 = 3 Rest 0
der nächste Schritt wäre nun :
( 3 / 2 = 1,5 ) ( 2 x 1 + 2 x 0,5 = 3)
da wir aber im binär nur ganze Dezimalzahlen verwenden dürfen lautet die nächste Zeile :
3 / 2 = 1 Rest 1
( 1 x 2 = 2, 3 - 2 = "1" )
1 / 2 = 0 Rest 1 <- MSB *
( 0 x 2 = 0 )
*LSB = Last significant Bit
*MSB = Most significant Bit
Der Binärcode für 192 wird nun vom MSB zum LSB abgelesen und zum besseren Verständniss nach 4 Ziffern wie folgt notiert :
1100 0000,
11000000,
ist trotzdem korrekt ! Nur schwerer zu lesen.
Björn
"Dieser Rechenweg funktioniert bis zu einer Zahl von 4294967295, aber warum das so ist kann ich nicht mehr erklären."
Der Algorithmus funktioniert natürlich auch darüber hinaus. Die angegebenen Zahl hätte als Ergebnis 32x die 1. (Als hexadezimal 8xF.) Wenn in dem Rechner nur 32-bit lange Zahlen gespeichert werden können, dann wäre das die Obergrenze, weil keine Zeichen mehr übrig sind. Auf dem Papier ist diese Grenze allerdings egal, ebenso wenn der Datentyp mehr als 32-bit zulässt.
Kevin
Also das mit der 4 Dezimalzahl verstehe ich nicht, bei mir kommt immer 4:2 = 2 Rest 0, 2:2= 1 Rest 1, 1:2=0 Rest 1, also wäre die Dualzahl doch 110 aber im System bei ihnen steht 100. Wie kann man das richtig Rechnen ?
Lina
Dir ist da nur ein kleiner Fehler unterlaufen.
4:2= 2 Rest 0
2:2=1 Rest 0 (weil da ja keine weitere Differenz ist, muss der Rest 0 sein)
1:2=0 Rest 1
Das ergibt dann 100
Helmut Mader
Mit 78 Jahren möchte ich meine alten Mathekenntnisse auffrischen, Deine Hilfe ist toll, weil klar und gut nachvollziehbar! Danke
Dori
Wie ermittle ich aber den rest? Woher weiß ich ob der Rest 1 oder 0 ist?
Sebastian
An Dori
Der Rest entsteht bei der Division.
0 = kein Rest vorhanden (2:2=1)
1 = Rest vorhanden (1:2=0.5)
Crispian
Gut
Crispian
Gute Rechnung
Übelst nachvollziehbar