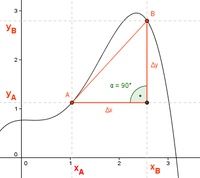
Herleitung des Differenzenquotienten
Um nun den Differenzenquotient des gegebenen Steigungsdreiecks zu ermitteln, bildet man den Quotienten aus Gegenkathete und Ankathete:
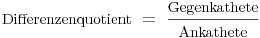
Berechnung des Differenzenquotienten
Die Ankathete kann in diesem Fall ermittelt werden, indem die Differenz der x-Werte von A und B gebildet wird:
Δx = xB - xA
Die Gegenkathete wird auf die gleiche Weise ermittelt, indem die Differenz der y-Werte von A und B gebildet wird:
Δy = yB - yA
Da die y-Werte die Funktionswerte f(x) der Funktion f sind, schreibt man auch:
Δy = f(xB) - f(xA)
Durch Einsetzen in die erste Gleichung erhält man den Differenzenquotient:
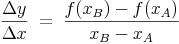
Winkel der Sekante
Der Winkel der Sekante entspricht dem Tangens des Differenzenquotients:
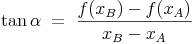
Durch Äquivalenzumformung dieser Gleichung kann der Winkel ermittelt werden:
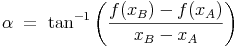
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar