Durchschnittsgeschwindigkeit

Die Durchschnittsgeschwindigkeit als Beispiel für die Verwendung des Differenzenquotienten.

Durchschnittsgeschwindigkeit berechnen

Durchschnittsgeschwindigkeit, Sekantensteigung Durchschnittsgeschwindigkeit

Die Sekantensteigung soll noch einmal am Beispiel der Durchschnittsgeschwindigkeit erläutert werden.

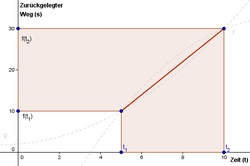
Ein Fahrzeug hat nach 5 Sekunden 10 Meter und nach 10 Sekunden 30 Meter zurück gelegt. Ermittle die durchschnittliche Geschwindigkeit, die das Fahrzeug in dieser Zeitspanne hatte.

1. Ermitteln der beiden Wertepaare

Wir bezeichnen die beiden Zeitpunkte t1=5s und t2=10s.

Weiters kennen wir den zurückgelegten Weg zum Zeitpunkt t1 und t

  • f(t1) = 10m
  • f(t2) = 30m

Daher erhält man die beiden geordneten Wertepaare: (5 | 10) und (10 | 30)

2. Berechnung der Differenzen

Im nächsten Schritt muss ermittelt werden, welche Zeit innerhalb dieses Intervalls verstrichen ist und wie viel Weg zurück gelegt wurde.

  • Die verstrichene Zeit in diesem Intervall ist somit:
    Δt = t2 - t1 = 10s - 5s = 5s
  • Der zurückgelegte Weg in diesem Intervall ist:
    Δs = f(t2) - f(t1) = 30m - 10m = 20m

3. Berechnen des Differenzenquotienten

Wie aus der Physik bekannt ist die Geschwindigkeit die Änderung des Weges in einer bestimmten Zeiteinheit:

\mbox{Geschwindigkeit}\ =\ \frac{\mbox{Zurückgelegter Weg}}{\mbox{Verstrichene Zeit}}
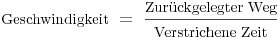
Die gleiche Formel mit den entsprechenden Abkürzungen lautet:
\bar{v}\ =\ \frac{\Delta s}{\Delta t}

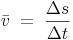
In unserem Fall kann man nun die Durchschnittsgeschwindigkeit berechnen:

\bar{v}\ =\ \frac{\Delta s}{\Delta t}\ =\ \frac{f(t_2)-f(t_1)}{t_2-t_1}\ = \frac{30m - 10m}{10s - 5s}\ = \frac{20m}{5s}\ =\ 4m/s

Anmerkung:

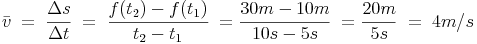
In der oben angeführten Abbildung, sind zwei Funktionen (f und g) abgebildet, die in diesem bestimmten Zeitraum eine Durchschnittsgeschwindigkeit von 4m/s haben. Beide Funktionen haben jedoch zu jedem Zeitpunkt zwischen t1 und t2 unterschiedliche Momentangeschwindigkeiten.

Kommentar verfassen