Momentangeschwindigkeit
Hier soll nochmals der Differentialquotient anhand eines Beispiels zur gleichmäßig beschleunigten Bewegung anschaulich gemacht werden. Eine gleichmäßig beschleunigte Bewegung ist eine Bewegung bei der sich die Geschwindigkeit in gleich großen Zeitabständen immer um das gleiche Maß a erhöht.
Dieser Koeffizient a ist ein Maß für die Beschleunigung und wird in m/s² angegeben. Erfährt ein Objekt eine Beschleunigung von 2m/s², so erhöht sich die Geschwindigkeit dieses Objekts jede Sekunde um 2m/s.
Die Funktion für die Zuordnung Weg-Zeit lautet:
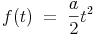
Die Steigung k an der Stelle t0 ist ein Maß für die Geschwindigkeit zum Zeitpunkt t0. Dies kann mit der Ableitung der Funktion f(t) nach f'(t) gelöst werden.
Wie bei der Behandlung des Differentialquotienten ausführlich erklärt wurde, muss der Grenzwert des Differenzenquotienten gebildet werden.
Ableitung
Den Differentialquotienten kennen wir bereits:
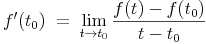
Nun setzen wir die oben angeführte Funktion ein und erhalten:
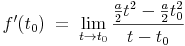
Die Konstante a ist ein Maß für die Beschleunigung, von der die Funktion nicht abhängig ist. Daher kann a/2 herausgehoben werden:
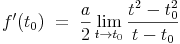
Im nächsten Schritt wird nun die dritte binomsche Formel angewendet, um (t2-t02) auzusplitten:
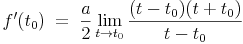
Daraus ergibt sich:
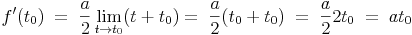
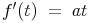
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Emma
Hallo sehr schön erlärt ich hätte mir jedoch noch eine Beispiel Rechnung gewünscht