Multiplizieren mit einer dekadischen Einheit

Multiplizieren einer Dezimalzahl mit einer dekadischen Einheit

Um eine Regel für die Multiplikation einer Dezimalzahl mit einer dekadischen Einheit herzuleiten, betrachten wir nochmals die Regel für die Multiplikation einer natürlichen Zahl mit einer dekadischen Einheit:

Beispiel 1:

Multipliziere 152 mit 10, mit 100 und mit 1000!

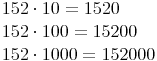
Bei der Multiplikation mit 10 wurde also eine 0, bei der Multiplikation mit 100 zwei 0 und bei der Multiplikation mit 1000 drei 0 an den ersten Faktor angehängt.

Die Stellenwerte wurden bei der Multiplikation mit 10, 100 und 1000 also nur um 1, 2 und 3 Stellen erhöht.

Eine Stellenwerterhöhung beim Rechnen mit Dezimalzahlen bedeutet nun, das Komma nach rechts zu verschieben.

Beim Multiplizieren mit 10 um 1 Stelle, beim Multiplizieren um 100 um 2 Stellen, beim Multiplizieren mit 1000 um 3 Stellen usw.

Beispiel 2:

Multipliziere 9,815 mit 10, mit 100 und mit 1000!

Multiplikation einer Dezimalzahl mit einer dekadischen Einheit:

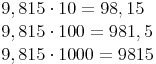
Multiplikation mit 10:
Komma um 1 Stelle nach rechts verschieben

Multiplikation mit 100:
Komma um 2 Stellen nach rechts verschieben

Multiplikation mit 1000:
Komma um 3 Stellen nach rechts verschieben

usw.

Eventuell müssen Nullen angehängt werden, um das Komma weiter verschieben zu können!