Multiplizieren von zwei negativen ganzen Zahlen
Hier wollen wir Ihnen erklären, wie man eine negative ganze Zahl mit einer weiteren negativen ganzen Zahl multipliziert.
Beispiel:
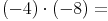
Wir versuchen eine logische Reihe von Multiplikationen mit (-8) zu bilden und beginnen (-8) der Reihe nach mit 3, 2, 1 und 0 zu multiplizieren:
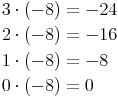
Wir können erkennen, dass das Ergebnis stets um 8 größer wird. Diese Reihe muss sich nur auch bei der Multiplikation mit negativen Zahlen so fortsetzen:
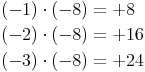
Nun vergleichen wir die Angabe des Beispiels mit dem Ergebnis, welches wir über die Addition bekommen haben:
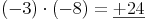
Zwei negative ganze Zahlen werden demnach einfach miteinander multipliziert. Das Ergebnis ist wiederum positiv, es steht also ein + davor.
Multipliziert man zwei negative ganze Zahlen miteinander, so ist das Ergebnis positiv.
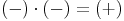
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
unbekant
ich konnt das leider nicht verstehen ? :/