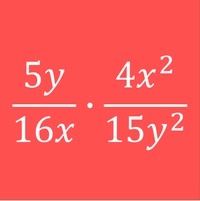Multiplizieren von Bruchtermen
Aus dem Kapitel "Brüche" wissen wir bereits, dass man Brüche multipliziert, indem man Zähler mit Zähler und Nenner mit Nenner multipliziert.
Tipp: Davor kann man eventuell auch noch kürzen!
Multiplizieren von Brüchen:
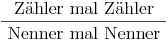
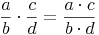
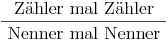
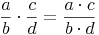
Dieses Wissen können wir auch auf Bruchterme anwenden. Auch hier ist es wichtig, dass die Nenner der beiden Brüche ungleich Null sind.
Bei den folgenden Beispielen setzen wir daher jeweils voraus, dass die Nenner der beiden Bruchterme ungleich Null sind!
Bsp. 1: Multiplikation eines Terms mit einem Bruchterm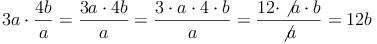
Bsp. 2: Multiplikation zweier Bruchterme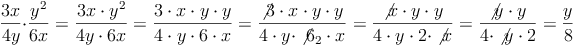
Bsp. 3: Multiplizieren von Bruchtermen mit Summen und Differenzen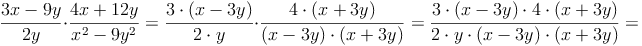
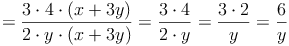
Multiplizieren von Bruchtermen:
Bruchterme werden multipliziert, indem man den Zähler mit dem Zähler und den Nenner mit dem Nenner multipliziert.
Beispiel:
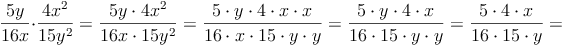
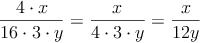
Tipps:
- Kürze immer so weit als möglich!
- Summen und Differenzen müssen vor dem Kürzen in Faktoren zerlegt werden!
Bruchterme werden multipliziert, indem man den Zähler mit dem Zähler und den Nenner mit dem Nenner multipliziert.
Beispiel:
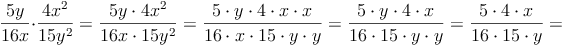
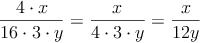
Tipps:
- Kürze immer so weit als möglich!
- Summen und Differenzen müssen vor dem Kürzen in Faktoren zerlegt werden!
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar