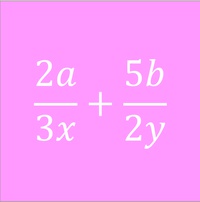Addieren und Subtrahieren von ungleichnamigen Bruchtermen
Von ungleichnamigen Bruchtermen spricht man dann, wenn die zu addierenden bzw. subtrahierenden Bruchterme unterschiedliche Nenner haben!
Aus dem Kapitel "Brüche" wissen wir bereits, dass man ungleichnamige Brüche zuerst auf denselben Nenner bringen muss (= gleichnamig machen). Dann addiert bzw. subtrahiert man, indem man die Zähler addiert bzw. subtrahiert und die Nenner unverändert lässt.
Um ungleichnamige Brüche addieren (bzw. subtrahieren) zu können, müssen die Brüche zuerst gleichnamig gemacht werden (auf den gleichen Nenner bringen).
Dazu ermittelt man den kleinsten gemeinsamen Nenner (= das kgV der Nenner ermitteln).
Anschließend werden die Zähler addiert (bzw. subtrahiert) und der Nenner unverändert gelassen.
Dieses Wissen können wir auch auf Bruchterme anwenden. Auch hier ist es wichtig, dass die Nenner der Brüche gleichnamig gemacht werden und ungleich Null sind.
Bei den folgenden Beispielen setzen wir daher jeweils voraus, dass die Nenner der Bruchterme ungleich Null sind!
Bsp.: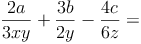
Erstelle dir nun eine Tabelle. Plane für jeden Nenner eine Zeile ein und eine weitere für den gemeinsamen Nenner.
Schreibe nun jeweils jeden Faktor in eine eigene Spalte - gleiche Zahlen bzw. Variablen untereinander:
| 3xy = 3 . x . y | 3 | x | y | ||
| 2y = 2 . y | 2 | y | |||
| 6z = 2 . 3 . z | 2 | 3 | z | ||
| Gemeinsamer Nenner | 2 | 3 | x | y | z |
Sieh dir nun den gemeinsamen Nenner an und vergleiche ihn mit den einzelnen Nennern. Die Bruchterme müssen nun mit den fehlenden Faktoren multipliziert werden.
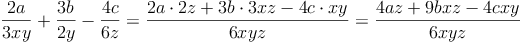
Um Bruchterme mit unterschiedlichen Nennern (= ungleichnamige Bruchterme) addieren oder subtrahieren zu können, müssen die Bruchterme zuerst auf den gleichen Nenner gebracht werden (= gleichnamig machen).
Anschließend werden die Zähler addiert (bzw. subtrahiert) und der Nenner unverändert gelassen.
Bsp.:
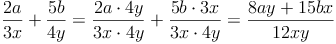
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar