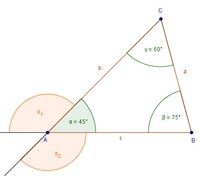
Ergänzung des Außenwinkel auf 180°
Verlängert man die Seiten eines Dreiecks, so entstehen bei jedem Winkel 2 Nebenwinkel (supplementäre Winkel = ergänzen einander auf 180°).
Zum Winkel 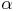 ergeben sich so also die Nebenwinkel
ergeben sich so also die Nebenwinkel 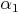 und
und 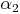 .
.
Die Winkel 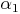 und
und 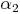 sind gleich groß und heißen Außenwinkel des Winkels
sind gleich groß und heißen Außenwinkel des Winkels 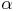 .
.
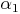 und
und 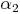 sind gleich groß und heißen Außenwinkel des Winkels
sind gleich groß und heißen Außenwinkel des Winkels 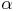 .
.
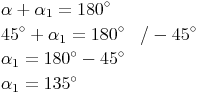
In jedem Dreieck gilt:
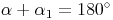
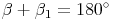
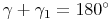
Winkel und Außenwinkel ergeben zusammen 180°.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar