Die Außenwinkel im Dreieck (II)
Wie wir bereits im Kapitel "Innenwinkel" festgestellt haben, gilt:
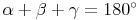
Wie wir bereits im Kapitel "Außenwinkel I" festgestellt haben, gilt:
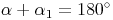
In der ersten Formel zählt man  zu
zu 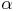 dazu, um 180° zu erhalten.
dazu, um 180° zu erhalten.
In der zweiten Formel zählt man 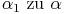 dazu, um 180° zu erhalten.
dazu, um 180° zu erhalten.
Das heißt,  sind zusammen genauso groß wie
sind zusammen genauso groß wie 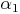 .
.
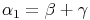
In jedem Dreieck gilt: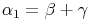
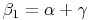
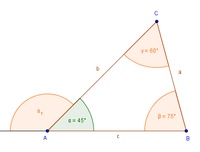
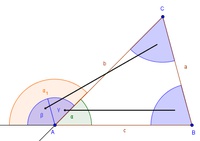
Jeder Außenwinkel ist genau so groß wie die Summe der beiden nicht anliegenden Innenwinkel.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
z
Die zeichnung ist eine bisschen klein ich verstehe nicht was aussenwinkel sin bitte hilfe .
Erich Hnilica, BEd
Liebe(r) z!
Unsere Zeichnungen lassen sich durch einfaches Anklicken vergrößern.
Die Beschreibung eines Außenwinkels findest du im vorhergehenden Kapitel "Außenwinkel".
Liebe Grüße
Erich Hnilica
Mathe-Lexikon-Team
Paskt
Danke das hat mir sehr geholfen.
Elitebabaren
Wie kann man sie bestimmen
Vanessa Otto
Ich verstehe nicht wie man auf das Ergebniss kommt also halt wie man es berechnet.
Würde mich freuen wenn ihr mir helfen könntet
Sequence
Gibt es eine Möglichkeit den Aussenwinkel, nur mit den zu Verfügung stehenden Innenwinkeln zu berechnen? Beispiels Beta = 25grad, Alpha = 15grad.
Hilfe
Es sollten schwerere Beispiele gezeigt werden