Kreisumfang

Der Umfang des Kreises

Herleitung der Formel:

Wir untersuchen, ob es einen Zusammenhang zwischen dem Kreisumfang und dem Durchmesser eines Kreises gibt.

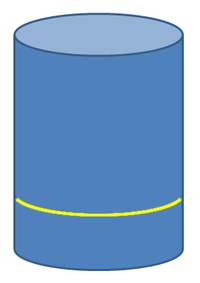
Von einem Zylinder messen wir uns zuerst mit einem Maßband den Umfang ab. Dieser ist zugleich auch der Umfang unseres Kreises. (= gelbe Kreislinie in unserer Skizze)

In unserem Beispiel beträgt dieser ca. 31,4 cm.

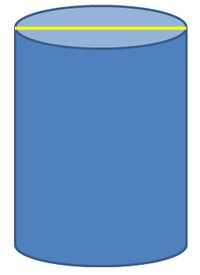
Die Querschnittsfläche eines Zylinders ist ein Kreis

Num messen wir uns von diesem Zylinder auch den Durchmesser ab, der gleichzeitig der Durchmesser unseres Kreises ist. (= gelbe Linie in unserer Skizze)

Wir erhalten einen Wert für den Durchmesser von 10 cm.

Vergleich:

Vergleicht man Umfang und Durchmesser mehrerer Kreise miteinander, so wird man erkennen, dass der Umfang ca. 3 Mal so groß ist wie der Durchmesser - und das bei jedem beliebigen Kreis!

Diesen Zusammenhang untersuchen wir genauer: 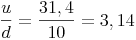$\frac{u}{d} = \frac{31,4}{10} = 3,14$

Diesen Zusammenhang können Sie mit jedem beliebigen Kreis versuchen, es kommt immer ein Ungefährwert von 3,14 heraus.

Diese Zahl wird als Kreiszahl 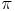$\pi$ bezeichnet. Sie ist eine irrationale Zahl (hat also unendlich viele Kommastellen): 3,14159265 ...

Umformen der Formel:

$\begin{align} & \frac{u}{d}=3,14 \\ & \frac{u}{d}= \pi\quad /\cdot d \\ & u = d \cdot \pi \\ \end{align}$

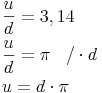
Nachdem gilt: 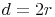d = 2r , kann man das d in der Formel auch durch 2r ersetzen: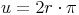 $u = 2r \cdot \pi$

Umfangsberechnung des Kreises:

Umfang = Durchmesser mal Pi
$u = d \cdot \pi$

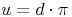
Umfang = 2 mal Radius mal Pi
$u = 2r \cdot \pi$

$\pi \approx 3,14159$
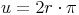
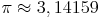
[sprich: pi]

Kreisumfang online berechnen

Durchmesser d

d =

Ergebnis: A = 706,858347058 m²

(Wert gerundet auf 4 Dezimalstellen: 706,8583 m²)

Der Lösungsweg im Detail:

Umrechnung Längenmaß

Schritt 1

Alle Angaben in gleiche Einheiten umwandeln

$d = 30.0\ \text{m} = 30.0\ \text{m}$

Kreisfläche

Schritt 2

Die Formel für den Flächeninhalt des Kreises lautet:

$A = r^2 \cdot \pi$

Allgemeines

Schritt 3

Da der Durchmesser bekannt ist lässt sich der Radius r ermitteln:

$r = \frac{d}{2} = \frac{30.0}{2} = 15.0$

Schritt 4

Setzt man die Werte ein, erhält man:

$A = 15.0^2 \cdot \pi$

A = 706.858347058

Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
3,6
121 Bewertungen

Kommentar #486 von Marlon 09.10.11 13:36 Marlon: ich hätte gern gewusst wie ich den Durchmesser errechne. Ich habe den Wert vom Umfang und möchte den Durchmesser ermitteln. Dies konnte ich leider nicht ganz finden.
Kommentar #7654 von Karla 18.05.13 12:54 Karla: Marlon, du musst nur die Formel für den Umfang umformen!
U=d*pi /:pi --> U:pi=d