Der Flächeninhalt des Kreises
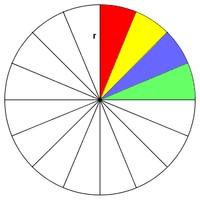
Formelherleitung:Wir konstruieren einen beliebig großen Kreis und unterteilen diesen in beliebig viele gleich große Teile.
In unserem Beispiel sind dies 16 gleich große Teile, die auch Kreissektoren genannt werden.
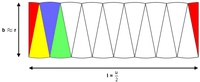
Wir zerschneiden nun die Kreisfläche in diese 16 Kreissektoren und legen 15 davon so nebeneinander, dass sie eine Figur ergeben, die einem Rechteck ähnelt. (Der 16. Teil wird halbiert und links und rechts angelegt.)
Wir berechnen nun den Flächeninhalt des Rechtecks, der ja genauso groß sein muss wie der Flächeninhalt des Kreises (die Fläche wurde ja nur anders angeordnet):
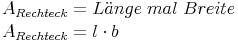
Die Breite des Rechtecks entspricht ungefähr dem Radius des Kreises:
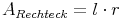
Die Länge des Rechtecks entspricht ungefähr dem halben Umfang des Kreises:
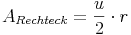
Die Umfangsformel wissen wir bereits aus dem vorherigen Kapitel: 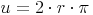 . Wir setzen diese statt dem u in die Formel ein:
. Wir setzen diese statt dem u in die Formel ein: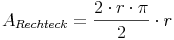
Da die Zahl 2 sowohl im Zähler als auch im Nenner vorkommt, kann man diese wegkürzen:
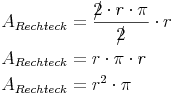
Flächeninhalt = Radius hoch 2 mal Pi
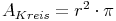
Kreisfläche online berechnen
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Milad
Danke sehr, das war sehr hilfreich verständlich