Bogenlänge

Um die Bogenlänge eines Kreissektors (Kreisausschnittes) zu berechnen, berechnet man das Produkt aus Radius, Pi und dem Zentriwinkel Alpha und dividiert dieses anschließend durch 180.

Die Bogenlänge eines Kreissektors berechnen

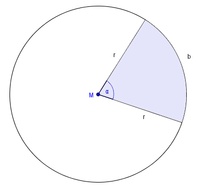
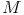M .......... Mittelpunkt

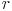r ........... Radius

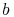b .......... Kreisbogen

\alpha .......... Zentriwinkel

Herleitung der Formel:

Aus dem vorherigen Kapitel kennen wir bereits die Formel zur Berechnung des Kreisumfangs (Zentriwinkel = 360°):

u = 2 \cdot r \cdot \pi

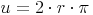
Der Kreisumfang entspricht der Bogenlänge eines Kreissektors mit dem Zentriwinkel 360°. Möchte man sich nun die Bogenlänge bei einem Zentriwinkel von 1° ausrechnen, so muss man die Formel durch 360 dividieren:

b = \frac {2 \cdot r \cdot \pi}{360}

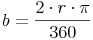
Möchte man die Bogenlänge bei einem Zentriwinkel von z.B. 75° ausrechnen, so muss man die Formel noch mit 75 multiplizieren. Wir nehmen allerdings statt 75 einen allgemeinen Wert, nämlich 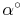\alpha^\circ - also mal Alpha:

b = \frac {2 \cdot r \cdot \pi \cdot \alpha}{360}

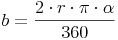
Kürzt man nun noch Zähler und Nenner durch 2, so ergibt sich:

b = \frac {2 \cdot r \cdot \pi \cdot \alpha}{360} = \frac {r \cdot \pi \cdot \alpha}{180}

Berechnung der Bogenlänge eines Kreissektors (Kreisausschnitts):

b = \frac {r \cdot \pi \cdot \alpha}{180}

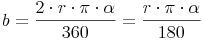
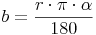
Bogenlänge = ( Radius mal Pi mal Zentriwinkel ) dividiert durch 180
Kommentar #7846 von guner 07.07.13 20:14
guner

sehr gut und präzise!

Kommentar #16318 von Markus 18.06.16 11:29
Markus

Wäre vielleicht noch hilfreich zu erwähnen, dass in der genannten Formel die Umrechnung von Grad in rad enthalten ist und dass die eigentliche Formel b=r*alpha [in rad] lautet.

Kommentar #16618 von Garvin 27.06.16 11:11
Garvin

Hallo,
leider habe nur den Radius, Höhe und Sehnenlänge als gegeben. Gerne hätte ich damit die Bogenlänge errechnet. Danke

Kommentar #18644 von Mohamed Sheikh Mohamud Ahmed 25.08.16 16:44
Mohamed Sheikh Mohamud Ahmed

Sehr gut

Kommentar #42270 von Hans 12.02.19 17:46
Hans

Bogenlänge Formel bitte

Kommentar #44902 von Alexander 15.12.20 21:03
Alexander

l (länge eines Seils an einer Rolle) = radius * Winkel (um den sich die Rolle gedreht hat, als Bogenmaß: [Winkel*2pi/360])

Kommentar #45032 von Die Mathematischen Mathematiker 14.01.21 11:22
Die Mathematischen Mathematiker

Hallo.
Wir sind Schülerchen einer Schule und haben nun von unserem Auftraggeber eine Aufgabe bekomme. Wir sollten herausfinden was die besagte Bogenlänge eines Mysteriößen Kreisausschnittes ist. Da der Inhalt unsere Köpfe leider nicht in der Lage war, eine Antwort zu formulieren und wir keine Lösung zur Hand hatten, sahen wir uns gezwungen uns andersweitig zu helfen. Da schoss uns die Grandiose Idee in unser Köpfchen, das "World Wide Web" zu benutzen. Nach mehrmaliger Recherche sind wir Prompt auf dieser Seite gelandet. Wir waren überwältig von dem angesamelten Wissen, dass uns das Mathe-Lexikon.at zur Verfüng stellte. An diesem Punkt waren wir wir uns eingig dass es unsere Bestimmung war, eine Lösung für diese Aufgabe zu finden. So konnten wir größere Auswikungen auf die Bevölkerung verhindern. Wir danken all unseren Fans die uns so tatkräftig unterstützt haben und wünschen allen ein gutes Rechnen.
Schwammige Grüße,
Die Tofu-Würstchen

Kommentar #45038 von Emma 14.01.21 14:45
Emma

Hallo gibt es bei der Bogenlänge eine Einheit?

Kommentar #45250 von Yoan 12.02.21 09:12
Yoan

Boa danke hatte im Unterricht nicht verstanden wie man das machen soll

Kommentar verfassen