Flächeninhalt

Um den Flächeninhalt eines Kreissektors (Kreisausschnittes) zu berechnen, berechnet man das Produkt aus dem Radius hoch 2, Pi und dem Zentriwinkel Alpha und dividiert dieses anschließend durch 360.

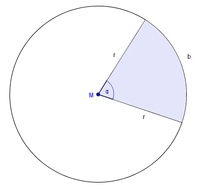
Den Flächeninhalt eines Kreissektors (Kreisausschnittes) berechnen

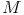M .......... Mittelpunkt

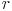r ........... Radius

\alpha .......... Zentriwinkel

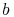b .......... Kreisbogen

Herleitung der Formel:

Aus dem vorherigen Kapitel kennen wir bereits die Formel zur Berechnung des Flächeninhaltes des gesamten Kreises (Kreisfläche):

A = r^2 \cdot \pi

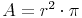
Ein ganzer Kreis entsteht dann, wenn der Zentriwinkel eine Größe von 360° hat. Beim Berechnen der Kreisfläche berechnet man also den Flächeninhalt eines Kreissektors mit dem Zentriwinkel 360°. Möchte man sich nun den Flächeninhalt eines Kreisausschnitts mit einem Zentriwinkel von 1° ausrechnen, so muss man die Formel durch 360 dividieren:

A = \frac {r^2 \cdot \pi}{360}

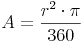
Möchte man die Fläche eines Kreisausschnitts mit einem Zentriwinkel von z.B. 62° ausrechnen, so muss man die Formel noch mit 62 multiplizieren. Wir nehmen allerdings statt 62 einen allgemeinen Wert, nämlich 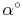\alpha^\circ - also mal Alpha: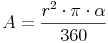

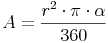
A = \frac {r^2 \cdot \pi \cdot \alpha}{360}

Berechnung des Flächeninhalts eines Kreissektors (Kreisausschnitts):

A = \frac {r^2 \cdot \pi \cdot \alpha}{360}

Flächeninhalt = ( Radius hoch 2 mal Pi mal Zentriwinkel ) dividiert durch 360

Kommentar verfassen