Flächeninhalt 2

Den Flächeninhalt eines Kreissektors (Kreisausschnitts) kann man sich berechnen, indem man sich das Produkt aus der Bogenlänge und dem Radius berechnet und durch 2 dividiert.

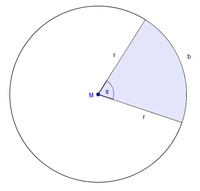
Den Flächeninhalt eines Kreissektors (Kreisausschnittes) berechnen, wenn der Radius und die Bogenlänge gegeben sind

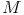M .......... Mittelpunkt

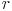r ........... Radius

\alpha .......... Zentriwinkel

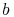b .......... Kreisbogen

Herleitung der Formel:

Aus dem vorherigen Kapitel kennen wir bereits die Formel zur Berechnung des Flächeninhaltes eines Kreissektors (Kreisabschnitts), wenn der Radius r und der Kreisbogen b gegeben sind:

A = \frac {r^2 \cdot \pi \cdot \alpha}{360}

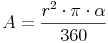
Statt 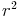r^2 schreiben wir nun wieder r \cdot r:

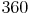Statt 360 schreiben wir nun 2 \cdot 180:

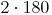Wir erinnern uns an die Formel zur Berechnung der Bogenlänge: 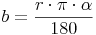b = \frac {r \cdot \pi \cdot \alpha}{180}

Betrachten wir unsere Flächeninhaltsformel genauer, so sehen wir, dass unsere Formel zur Berechnung der Bogenlänge 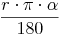\frac {r \cdot \pi \cdot \alpha}{180} in der Flächeninhaltsformel steckt, also kann man sie durch das Ergebnis 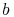b ersetzen:

Berechnung des Flächeninhalts eines Kreissektors (Kreisausschnitts):

A = \frac {b \cdot r}{2}

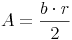
Flächeninhalt = ( Bogenlänge mal Radius ) dividiert durch 2

Kommentar verfassen