Zentriwinkel / Randwinkel

Der Zentriwinkel eines Kreises ist doppelt so groß wie sein zugehöriger Randwinkel.

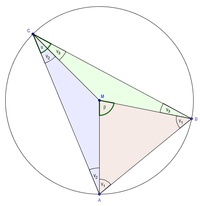
Zusammenhang zwischen dem Zentriwinkel und dem Randwinkel eines Kreises

Wir konstruieren einen Kreis mit beliebigem Radius.

Auf der Kreislinie wählen wir 3 beliebige Punkte A, B und C.

Wir verbinden nun die 3 konstruierten Punkte jeweils mit dem Mittelpunkt, dann der Reihe nach von A nach B nach C und wieder nach A.

Dadurch entstanden 3 gleichschenklige Dreiecke in denen die Basiswinkel jeweils gleich groß sind (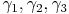 $\gamma_1 , \gamma_2 , \gamma_3$ ).

Beweis, dass der Zentriwinkel 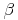$\beta$ doppelt so groß ist wie sein zugehöriger Randwinkel $\alpha$ :

Winkelsummensatz im Dreieck ABM: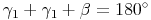
$\gamma_1 + \gamma_1 + \beta = 180^\circ$
$2\gamma_1 + \beta = 180^\circ\qquad / - \beta$
$2\gamma_1 = 180^\circ - \beta$

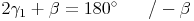
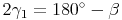
Winkelsummensatz im Dreieck ABC: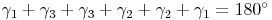
$\gamma_1 + \gamma_3 + \gamma_3 + \gamma_2 + \gamma_2 + \gamma_1 = 180^\circ$
$2\gamma_1 + 2\gamma_2 + 2\gamma_3 = 180^\circ$

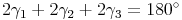
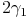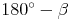Nun erstezen wir $2\gamma_1$ durch $180^\circ - \beta$ :
$180^\circ - \beta + 2\gamma_2 + 2\gamma_3 = 180^\circ$

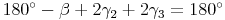
Umformen: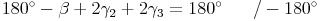
$180^\circ - \beta + 2\gamma_2 + 2\gamma_3 = 180^\circ\qquad / - 180^\circ$
$- \beta + 2\gamma_2 + 2\gamma_3 = 0\qquad / + \beta$
$2\gamma_2 + 2\gamma_3 = \beta$

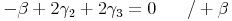
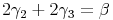
Herausheben: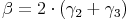
$\beta = 2 \cdot (\gamma_2 + \gamma_3)$

Aus der Skizze erkennen wir, dass $\gamma_2 + \gamma_3$ den Winkel $\alpha$ ergeben:
$\beta = 2 \cdot (\gamma_2 + \gamma_3)$
$\beta = 2 \cdot \alpha$

Der Zentriwinkel eines Kreises ist doppelt so groß wie sein zugehöriger Randwinkel:

$\beta = 2 \cdot \alpha$

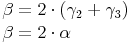
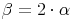
Dieser Artikel hat mir geholfendas half mir
Dieser Artikel hat mir nicht geholfen... leider nicht
Kommentar zu dieser Seite abgebenKommentar
Frage im Forum stellenForum
Offizielle Facebook-SeiteFacebook

Kommentar schreiben

Kommentare zu diesem Thema