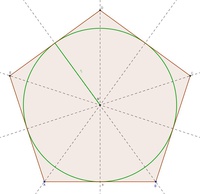
Der Inkreis eines regelmäßigen Fünfecks
Zu jedem regelmäßigen Vieleck lässt sich ein Inkreis zeichen.
Um den Inkreismittelpunkt zu erhalten, zeichen wir mindestens zwei Winkelsymmetralen. In unserem Beispiel wurden der Genauigkeit halber alle fünf Winkelsymmetralen gezeichnet.
Um den Inkreisradius zu erhalten, halbieren wir eine beliebige Seite des regelmäßigen Vielecks und verbinden diesen Punkt mit dem Mittelpunkt.
Da man nun den Radius erhalten hat, kann man nun auch den Inkreis konstruieren.
Der Inkreis eines regelmäßigen Fünfecks
Zu jedem regelmäßigen Fünfeck lässt sich ein Inkreis zeichnen.
Der Inkreismittelpunkt ist der Schnitpunkt der Winkelsymmetralen, der Inkreisradius ist die kürzeste Verbindung des Inkreismittelpunktes mit dem Mittelpunkt einer Seite des regelmäßigen Fünfecks.
Zu jedem regelmäßigen Fünfeck lässt sich ein Inkreis zeichnen.
Der Inkreismittelpunkt ist der Schnitpunkt der Winkelsymmetralen, der Inkreisradius ist die kürzeste Verbindung des Inkreismittelpunktes mit dem Mittelpunkt einer Seite des regelmäßigen Fünfecks.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar