Die Körperhöhe h eines Kegels
Als Körperhöhe wird die kürzeste Verbindung vom Mittelpunkt des Kreises der Grundfläche zur Spitze des Kegels bezeichnet.
Die Körperhöhe wird mit h bezeichnet und steht somit im rechten Winkel auf die Grundfläche.
Die Mantellinie s entspricht NICHT der Körperhöhe h des Zylinders!
Die Körperhöhe berechnen
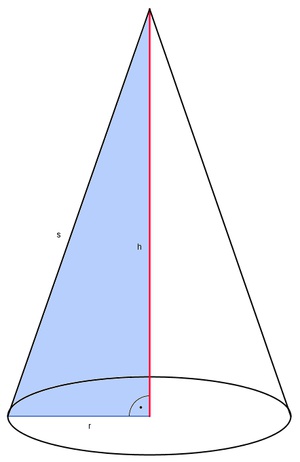
Radius r, Mantellinie s und Höhe h bilden ein rechtwinkeliges Dreieck.
Sind der Radius r (entspricht der Kathete a) und die Länge der Mantellinie s (entspricht der Hypotenuse c) eines Kegels bekannt, so kann man mit Hilfe des Lehrsatzes des Pythagoras die Länge der Körperhöhe h (entspricht der Kathete b) berechnen.
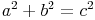

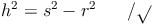
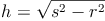
Die Körperhöhe h
Als Körperhöhe h wird die kürzeste Verbindung vom Mittelpunkt des Kreises der Grundfläche zur Spitze des Kegels bezeichnet.
Die Körperhöhe steht normal auf die Grundfläche.
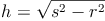
Als Körperhöhe h wird die kürzeste Verbindung vom Mittelpunkt des Kreises der Grundfläche zur Spitze des Kegels bezeichnet.
Die Körperhöhe steht normal auf die Grundfläche.
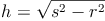
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Nicki Minaj
supiiii
Dmitri Ivanovich Mendeleev
geht