Das Volumen (der Rauminhalt) des Kegels
Unter dem Volumen (oder auch Rauminhalt) eines Körpers versteht man den räumlichen Inhalt dieses Körpers.
Umgangssprachlich würde man sagen: all jenes, das in diesen Zylinder hineinpasst (Flüssigkeit, ...)
Das Volumen wird mit V abgekürzt und entspricht in der ebenen Geometrie dem Flächeninhalt.
Herleitung der Formel:
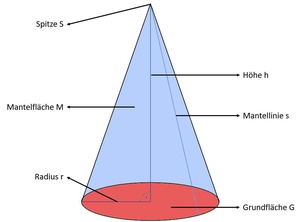
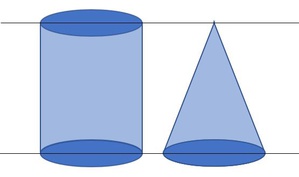
Wir gehen von einen Zylinder und einem Kegel aus, die dieselbe Grundfläche (=Kreis) und dieselbe Höhe besitzen.
Aus dem Kapitel Volumen des Zylinders kennen wir bereits die Formel zur Berechnung des Volumens eines Zylinders:
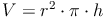
Umschüttversuch:
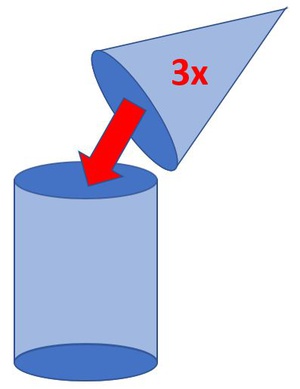
Wir füllen nun den Kegel mit Flüssigkeit und schütten diese in den Zylinder mit gleicher Grundfläche und gleicher Höhe.
Diesen Vorgang kann man genau 3 Mal machen bis der Zylinder ganz voll ist.
Das Volumen des Zylinders ist daher 3 Mal so groß wie das Volumen des Kegels.
Oder anders ausgedrückt:
Das Volumen des Kegels ist ein Drittel des Volumens des Zylinders.
Somit müssen wir nur die Volumsformel des Zylinders durch 3 dividieren, um die Volumsformel des Kegels zu erhalten:
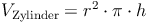
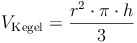
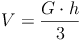
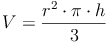
Volumen = (Grundfläche mal Höhe) : 3
Beispiel:
geg.: Kegel: r = 7 cm , h = 12 cm
ges.: V
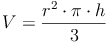
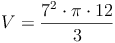
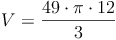
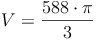
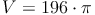
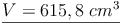
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Nicki Minaj
ECHT gute Erklärungen *klatscht*
Jörn
Die Herleitung des Kegelvolumens durch das dreifache Einschüttens in den Zylinder setzt natürlich voraus, dass man 1/3-Verhältnis bereits kennt. Das ist natürlich keine Herleitung, Erklärung, Begründung o.Ä.
Franz Maierhuber
Das ist zwar eine schön anschauliche Darstellung, aber keine Herleitung!
Janvi
die Herleitung ist auch für Hauptschüler, der Abiturent müsste das 3 fache Volumen beweisen