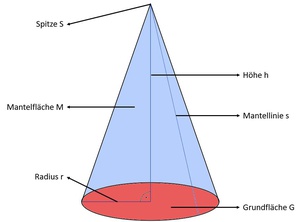
Die Oberfläche des Kegels
Im Kapitel Netz eines Kegels haben wir bereits erläutert, dass die Grundfläche eines Kegels ein Kreis und die Mantelfläche ein Kreisausschnitt ist.
Diese zwei Flächen bilden also die Oberfläche des Kegels.
Um die Oberfläche des Kegels zu berechnen, muss man also diese zwei Flächen (Kreis und Kreisausschnitt) addieren:
Oberfläche = Grundfläche (Kreis) + Mantelfläche (Kreisausschnitt)
Als Formel geschrieben:
O = G + M
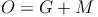
Herleitung der Formel
1) Grundfläche:
Die Grundfläche eines Kegels ist ein Kreis.
Die Flächeninhaltsformel eines Kreises kennen wir bereits aus dem Kapitel :
Somit gilt: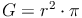
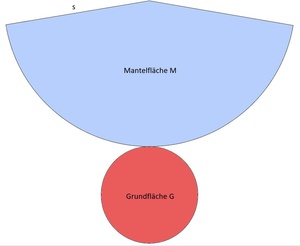
2) Mantelfläche:
Die Mantelfläche eines Kegels ist ein Kreisausschnitt.
Die Flächeninhaltsformel eines Kreisausschnittes kennen wir bereits aus dem Kapitel Flächeninhalt eines Kreisausschnittes :
Die Bogenlänge b des Kreisausschnittes entspricht dem Umfang des Kreises der Grundfläche.
Die Formel zur Berechnung des Kreisumfanges kennen wir bereits aus dem Kapitel Umfang des Kreises :
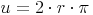
Somit gilt: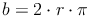
Der Radius r des Kreisausschnittes entspricht der Mantellinie s des Kegels:
Zusammenfassung:
Nun setzen wir statt b folgendes ein: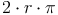 
Für r setzten wir s ein.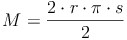
Abschließend kann noch durch 2 gekürzt werden, es bleibt: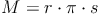 
3) Zusammenfassung:
Oberfläche = Grundfläche + Mantelfläche
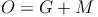
Für G setzten wir folgendes ein: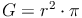
Für M setzten wir folgendes ein: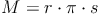
Daraus ergibt sich: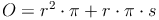
Die Oberfläche eines Kegels setzt sich aus der Grundfläche und der Mantelfläche zusammen:
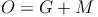
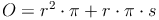
Beispiel:
Ein Kegel hat einen Radius von r = 4cm und eine Mantellinie von s = 10 cm. Berechne die Oberfläche!
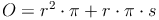
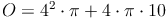
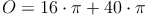
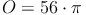
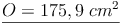
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Leon Franken
Gibt es noch eine alternative Formel?