Das Volumen (der Rauminhalt) des Zylinders
Unter dem Volumen (oder auch Rauminhalt) eines Körpers versteht man den räumlichen Inhalt dieses Körpers.
Das Volumen entspricht in der ebenen Geometrie dem Flächeninhalt.
Herleitung der Formel:
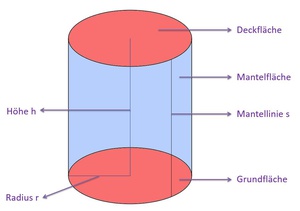
Die Grundfläche des Zylinders ist ein Kreis. Legt man jetzt mehrere (viele) Kreise übereinander, so entsteht ein Zylinder.
Die Höhe h gibt dabei an, wie hoch diese Kreise übereinander gelegt wurden.
Das Volumen des Kreises lässt sich also berechnen, indem man die Grundfläche mit der Höhe multipliziert: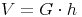
Um das Volumen zu berechnen benötigen wir also zuerst den Flächeninhalt der Grundfläche. Die Grundfläche ist ein Kreis:
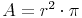
Nun setzten wir in der Formel 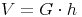 die Flächeninhaltsformel des Kreises für die Grundfläche G ein und erhalten damit:
die Flächeninhaltsformel des Kreises für die Grundfläche G ein und erhalten damit: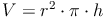
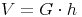
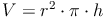
Volumen = Grundfläche mal Höhe
Beispiel:
geg.: Zylinder: r = 7 cm , h = 12 cm
ges.: V
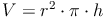

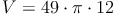
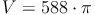
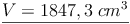
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
birkner
geil, das internet, alles was man seit der schule vergessen hat, kann man hier wiederfinden,