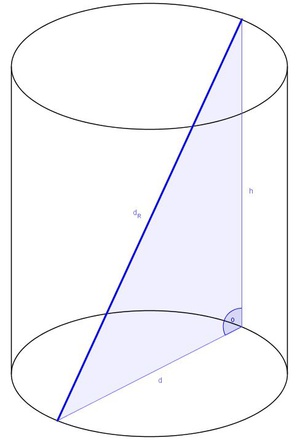
Die Raumdiagonale des Zylinders
Eine Raumdiagonale des Zylinders verbindet einen beliebigen Punkt der Kreislinie der Grundfläche mit dem am weitesten entfernten (= gegenüberliegenden) Punkt der Kreislinie der Deckfläche.
Nachdem es unendlich viele Punkte auf der Kreislinie der Grundfläche gibt, gibt es auch unendlich viele Raudiagonalen, die allerdings gleich lang sind.
Mit Hilfe des Lehrsatzes des Pythagoras lässt sich die Länge der Raumdiagonale eines Zylinders sehr einfach berechnen, wenn auch der Durchmesser (oder Radius) sowie die Höhe des Zylinders bekannt sind.
Beispiel:
Von einem Zylinder kennt man den Durchmesser d = 12 cm und die Höhe h = 15 cm.
Berechnen Sie die Länge der Raumdiagonale!
Herleitung der Formel:
Zeichnet man die Raumdiagonale sowie den Durchmesser und die Höhe in einem Zylinder ein, so kann man gut erkennen, dass ein rechtwinkeliges Dreieck gebildet wird.
In jedem rechtwinkeligen Dreieck gilt der Lehrsatz des Pythagoras:
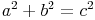
Die beiden Katheten a und b entsprechen in unserem Beispiel dem Durchmesser d der Grundfläche sowie der Höhe h des Zylinders.
Die Hyotenuse c entspricht der Raudiagonale 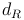 .
.
Wir ersetzen nun also diese Werte: 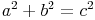
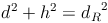
Umdrehen und Wurzelziehen: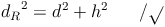
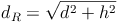
Beispiel (Forts.):
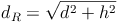
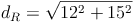
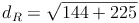
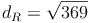
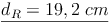
Eine Raumdiagonale des Zylinders verbindet einen beliebigen Punkt der Kreislinie der Grundfläche mit dem am weitesten entfernten (= gegenüberliegenden) Punkt der Kreislinie der Deckfläche.
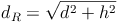
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar