Die Oberfläche des Zylinders

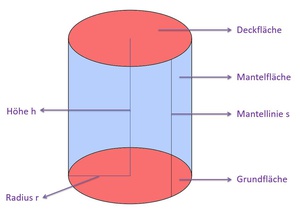
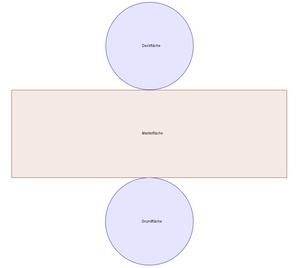
Im Kapitel Netz eines Zylinders haben wir bereits erläutert, dass die Grundfläche und die Deckfläche eines Zylinders 2 gleich große Kreise sind und die Mantelfläche ein Rechteck ist.

Diese 3 Flächen bilden also die Oberfläche des Zylinders.

Um die Oberfläche des Zylinders zu berechnen, muss man also diese 3 Flächen (2 gleich große Kreise und Rechteck) addieren:

Oberfläche = Grundfläche + Deckfläche + Mantelfläche

Da Grund- und Deckfläche gleich groß sind, gilt: Grundfläche = Deckfläche

Oberfläche = 2 mal Grundfläche + Mantelfläche

Als Formel geschrieben:

O = 2G + M

Oberfläche eines Zylinders

O = 2G + M

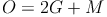
Herleitung der Formel

1) Grundfläche und Deckfläche:

Die Grund- und Deckfläche eines Zylinders sind zwei gleich große Kreise.

Die Flächeninhaltsformel eines Kreises kennen wir bereits aus dem Kapitel Kreisfläche :

$A_\text{Kreis} = r^2 \cdot \pi$

Da die Oberfläche eines Zylinders aus 2 Kreisen besteht, gilt: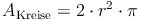
$A_\text{Kreise} = 2 \cdot r^2 \cdot \pi$

2) Mantelfläche:

Die Mantelfläche eines Zylinders ist ein Rechteck.

Die Länge dieses Rechtecks entspricht dem Umfang des Kreises der Grund- bzw. Deckfläche.

Umfangsformel des Kreises: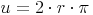 $u = 2 \cdot r \cdot \pi$

Da die Länge des Umfangs der Länge des Rechtecks entspricht, gilt: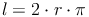
$l = 2 \cdot r \cdot \pi$

Die Breite dieses Rechtecks entspricht der Höhe des Zylinders. Somit gilt:
b = h

Flächeninhaltsformel des Rechtecks: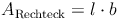
$A_\text{Rechteck} = l \cdot b$

Nun setzen wir für 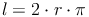$l = 2 \cdot r \cdot \pi$ und für b = h in diese Formel ein:

$A_\text{Rechteck} = 2 \cdot r \cdot \pi \cdot h$

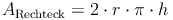
3) Zusammenfassung:

Oberfläche = Grundfläche + Deckfläche + Mantelfläche

Oberfläche = 2 mal Grundfläche + Mantelfläche

O = 2G + M
$O = 2 \cdot r^2 \cdot \pi + 2 \cdot r \cdot \pi \cdot h$

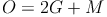
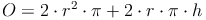
Durch Herausheben von 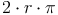$2 \cdot r \cdot \pi$ kann die Formel noch vereinfacht werden: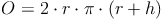
$O = 2 \cdot r \cdot \pi \cdot (r + h)$

Oberfläche des Zylinders:

Die Oberfläche eines Zylinders setzt sich aus der Grundfläche, der Deckfläche und der Mantelfläche zusammen:

$O = 2 \cdot G + M$
$O = 2 \cdot r^2 \cdot \pi + 2 \cdot r \cdot \pi \cdot h$
$O = 2 \cdot r \cdot \pi \cdot (r +h)$

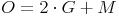
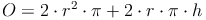
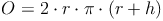
Beispiel:

Ein Zylinder hat einen Radius von r = 4cm und eine Höhe von h = 10 cm. Berechne die Oberfläche!

1. Möglichkeit: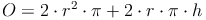

$O = 2 \cdot r^2 \cdot \pi + 2 \cdot r \cdot \pi \cdot h$

$O = 2 \cdot 4^2 \cdot \pi + 2 \cdot 4 \cdot \pi \cdot 10$

$O = 32 \cdot \pi + 80 \cdot \pi$

$O = 112 \cdot \pi$

$\underline{O = 351,9\ cm^2}$

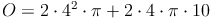
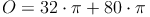
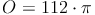
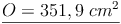
2. Möglichkeit: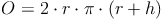

$O = 2 \cdot r \cdot \pi \cdot (r + h)$

$O = 2 \cdot 4 \cdot \pi \cdot (4 + 10)$

$O = 8 \cdot \pi \cdot 14$

$O = 112 \cdot \pi$

$\underline{O = 351,9\ cm^2}$

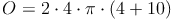
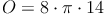
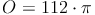
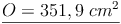
Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
3,2
53 Bewertungen

Kommentar #43626 von Alex 07.03.20 10:31 Alex: NICHT HILFREICH ZUM LERNEN UND AUCH ZUM VERSTEHEN
Kommentar #44856 von nunu 09.12.20 08:26 nunu: Ich hätte da gern noch eine Frage. Wie wäre die Formel wenn mir nur Höhe und Mantelfläche angegeben werden

Oberfläche des Zylinders

Die Oberfläche des Zylinders

Herleitung der Formel

Beispiel:

Kommentar verfassen

Ähnliche Arbeitsblätter