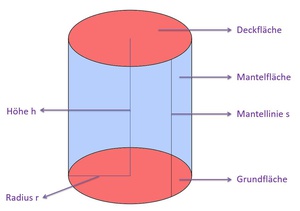
Formeln für Berechnungen im Zylinder
Hier finden Sie eine Zusammenfassung der wichtigsten Formeln für Berechnungen im Zylinder.
Der Radius wird mir r bezeichnet, der Durchmesser mit d, Die Mantellinie mit s und die Höhe mit h.
Mantelfläche:
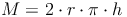
Oberfläche:
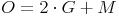
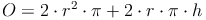
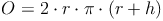
Oberfläche - Umkehraufgaben:
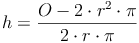
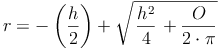
Volumen:
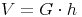
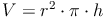
Volumen - Umkehraufgaben:
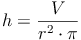
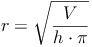
Raumdiagonale:
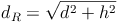
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar