Umkehraufgabe zum Volumen des Kegels: Berechnung des Radius r

Hier finden Sie eine Formel, wie Sie den Radius r eines Kegels berechnen können, wenn Sie das Volumen und seine Höhe kennen.

Berechnung des Radius des Kegels, wenn das Volumen und die Höhe bekannt sind

Beispiel

Ein Kegel hat ein Volumen von 117,3 cm³ und eine Höhe von 7 cm.

Berechnen Sie den Radius des Kegels!

Herleitung der Formel

Aus dem Kapitel  wissen wir bereits, dass sich das Volumen des Kegels aus dem Drittel des Produktes von Grundfläche (=Kreis) mal Höhe errechnet. Daraus ergibt sich folgende Formel:

Wiederholung: Das Volumen (der Rauminhalt) des Kegels:

V = \frac{G \cdot h}{3}

V = \frac{r^2 \cdot \pi \cdot h}{3}

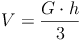
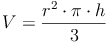
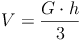
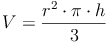
Nachdem wir allerdings das Volumen und die Höhe des Kegels kennen, nicht aber den Radius, müssen wir die Formel so umformen, dass r (der Radius) alleine auf einer Seite steht:

V = \frac{r^2 \cdot \pi \cdot h}{3}\qquad / \cdot 3

3 \cdot V = r^2 \cdot \pi \cdot h\qquad / : (\pi \cdot h)

\frac{3 \cdot V}{\pi \cdot h} = r^2\qquad / \sqrt

\sqrt{\frac{3 \cdot V}{\pi \cdot h}} = r

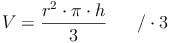
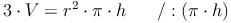
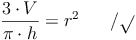
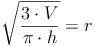
Beispiel (Fortsetzung)

r = \sqrt{\frac{3 \cdot V}{\pi \cdot h}}

r = \sqrt{\frac{3 \cdot 117,3}{\pi \cdot 7}}

r = \sqrt{\frac{351,9}{22}}

r = \sqrt{16}

\underline{r = 4\ cm}

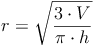
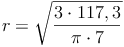
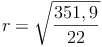
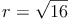
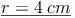
Probe: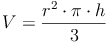

V = \frac{r^2 \cdot \pi \cdot h}{3}

V = \frac{4^2 \cdot \pi \cdot 7}{3}

V = \frac{16 \cdot \pi \cdot 7}{3}

V = \frac{112 \cdot \pi}{3}

V = \frac{351,9}{3}

V = 117,3\ cm^3

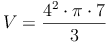
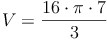
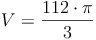
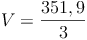
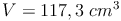
Antwort:

Der Kegel hat einen Radius von 4 cm.

Berechnung des Radius eines Kegels, wenn Volumen und Höhe bekannt sind:

r = \sqrt{\frac{3 \cdot V}{\pi \cdot h}}

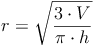
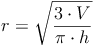
Radius = Quadratwurzel aus [ (3 mal Volumen) : (Pi mal Höhe ]

Kommentar verfassen