Das Volumen der dreiseitigen Pyramide
Unter dem Volumen versteht man den Rauminhalt eines Körpers, also z.B. jene Flüssigkeit, die ich in einen Körper füllen kann.
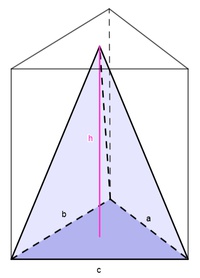
Um die Formel zur Berechnung des Volumens einer dreiseitigen Pyramide besser zu verstehen, zeichnen wir ein Prisma mit derselben Grundfläche und derselben Höhe um die dreiseitige Pyramide.
Füllt man nun den Rauminhalt der Pyramide in das Prisma (Umfüllversuch), so kann man das genau 3 Mal machen. Das Volumen des Prismas (V = G . h) ist also 3 Mal so groß wie jenes der Pyramide oder umgekehrt:
Das Volumen einer Pyramide ist immer ein Drittel des Volumens eines Prismas mit gleicher Grundfläche und Höhe.
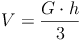
Grundfläche = rechtwinkeliges Dreieck:
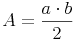
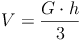
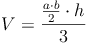
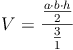
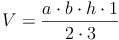
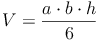
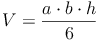
Grundfläche = allgemeines Dreieck:
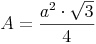
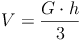
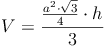
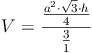
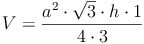
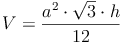
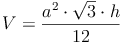
Grundfläche = gleichschenkeliges Dreieck:
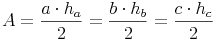
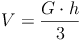
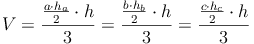
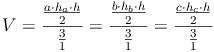
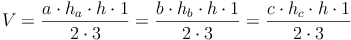
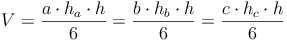
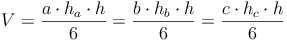
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Inormativ
Ihr meint das Volumen eines beliebigen Dreiecks in der letzten Box?!
Free Palastine
Das hat schon geholfen aber am besten wäre es mit alle Formeln nur Volum würde es nicht ausreichen.