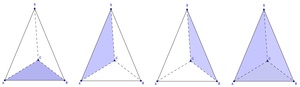
Die Seitenflächen der dreiseitigen Pyramide
Ein geometrischer Körper wird von Flächen begrenzt.
Bei der dreiseitigen Pyramide handelt es sich hierbei um insgesamt 4 Flächen.
Die unterste Fläche nennt man Grundfläche, welche die Form eines allgemeinen Dreiecks hat.
Die 3 verbleibende Flächen werden als Seitenflächen bezeichnet. Sie bilden zusammen den Mantel.
Die Seitenflächen sind 3 unterschiedlich große gleichschenklige Dreiecke (bei einer geraden Pyramide) oder allgemeine Dreiecke (bei einer schiefen Pyramide).
Sonderformen:
Ist die Grundfläche ein gleichseitiges Dreieck (= alle Seiten des Dreiecks sind gleich lang), so sind die 3 Seitenflächen gleiche gleichschenklige Dreiecke und somit gleich groß.
Ist die Grundfläche ein gleichschenkliges Dreieck (= 2 Seiten des Dreiecks sind gleich lang), so sind 2 Seitenflächen gleiche gleichschenklige Dreiecke und somit gleich groß.
Eine dreiseitige Pyramide wird von einem allgemeinen Dreieck als Grundfläche und 3 gleichschenkligen Dreiecken (bei einer geraden Pyramide) bzw. 3 allgemeinen Dreiecken (bei einer schiefen Pyramide), die zusammen den Mantel bilden, begrenzt.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar