Kartesisches Produkt

Es seien A und B Mengen. Das kartesische Produkt A x B ist die Menge aller geordneten Paare (a,b), wobei a ein Element der Menge A und b ein Element der Menge b ist.

Kartesisches Produkt

Es seien A und B Mengen. Das kartesische Produkt A x B ist die Menge aller geordneten Paare (a,b), wobei a ein Element der Menge A und b ein Element der Menge B ist.
A{\times}B=\{(a,b)\ \mid\ (a{\in}A)\ {\wedge}\ (b{\in}B)\}

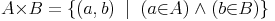
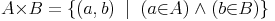
Beispiel 1:
A=\{1,2,3\};\ B=\{1,2\}

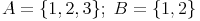
Das kartesische Produkt lautet daher:

A{\times}B=\{(1,1),(1,2),(2,1),(2,2),(3,1),(3,2)\}

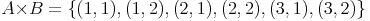
(3,1) ist in diesem Fall ein Element des kartesischen Produkts und wird auch Tupel genannt.

Beispiel 2:
D=\{Mo,Di,Mi\};\ E=\{0,1\}

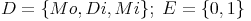
Das kartesische Produkt DxE lautet:

D{\times}E=\{(Mo,0),(Mo,1),(Di,0),(Di,1),(Mi,0),(Mi,1)\}

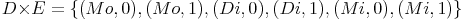
Das kartesische Produkt ExD lautet jedoch:
E{\times}D=\{(0,Mo),(0,Di),(0,Mi),(1,Mo),(1,Di),(1,Mi)\}

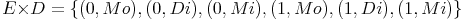
Daraus folgt: Für das kartesische Produkt gilt das Kommutativgesetz nicht.

Kommentar #7798 von Matheboy 21.06.13 09:00
Matheboy

Das kartesische Produkt ExD lautet jedoch:

hier muss ExD stehen, anstelle von DxE

peace out

Kommentar #7850 von Alex 13.07.13 09:27
Alex

Das kartesische Produkt ExD lautet jedoch:
D{\times}E=\{(0,Mo),(0,Di),(0,Mi),(1,Mo),(1,Di),(1,Mi)\}

Also sollte es auch bei der Menge richtig stehen.

Kommentar #7856 von admin 15.07.13 08:14
admin

Danke für den Hinweis. Wir haben den Tippfehler soeben korrigiert.

Kommentar verfassen