Komplementärmenge
Wenn bei einer Mengendefinition eine Grundmenge M angegeben wird, so enthält die Komplementärmenge A' alle Elemente der Grundmenge M, die kein Element der Menge A sind.
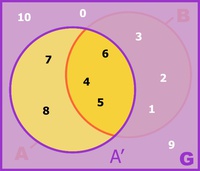
Die mathematische Schreibweise dafür lautet:
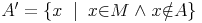
Beispiel:
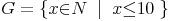
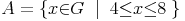
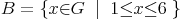
Die Komplementärmenge A' enthält somit alle Zahlen, die nicht in A enthalten sind. In der nebenstehenden Abbildung ist der entsprechende Bereich farblich hervorgehoben. Die Komplementärmenge A' ergibt bei diesem Beispiel (aufzählend):
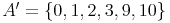
(oder beschreibend):
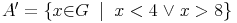
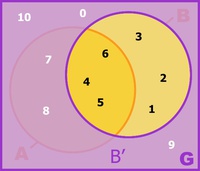
Die Komplementärmenge B' ergibt:
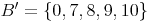
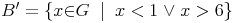
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar