Differenz (Differenzmenge)
Gegeben seien zwei Mengen (A,B). Die Differenzmenge A\B ist die Menge all jener Elemente, die in A aber nicht in B enthalten sind.
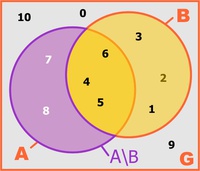 Differenzmenge A\B
Differenzmenge A\B
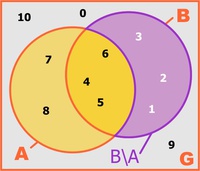 Differenzmenge B\A
Differenzmenge B\A
Die mathematische Schreibweise dafür lautet:
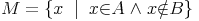
Beispiel:
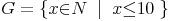
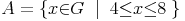
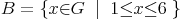
Die Differenzmenge A\B enthält die Zahlen 7 und 8, da diese in der Menge A, aber nicht in der Menge B enthalten sind. In der nebenstehenden Abbildung (Abb. I) ist der entsprechende Bereich farblich hervorgehoben. Die Differenzmenge A\B ergibt bei diesem Beispiel (aufzählend):
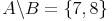
(oder beschreibend):
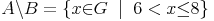
Wichtig: Für die Operation Differenz gilt weder das Kommutativgesetz und noch das Assoziativgesetz .
Das bedeutet, dass die Differenz B\A ein anderes Ergebnis liefert als A\B (Siehe auch Abb. II):
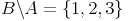
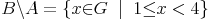
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar