Ganze Zahlen
Die Menge der ganzen Zahlen ist die Menge aller positiven und negativen ganzen Zahlen.
Z = {... -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...}
Ganze Zahlen - Abgeschlossene Operationen
Bei den ganzen Zahlen sind die Addition, die Multiplikation und auch die Subtraktion abgeschlossene Operationen (Die nachfolgenden Beispiele sollen dies veranschaulichen, sind aber keine vollständigen Beweise! Auf diese wurde aus Gründen der Verständlichkeit verzichtet)
Addition:
Die Summe zweier ganzer Zahlen ergibt immer eine ganze Zahl
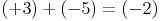
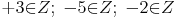
Multiplikation:
Das Produkt zweier ganzer Zahlen ergibt immer eine ganze Zahl
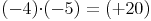
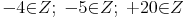
Subtraktion:
Die Differenz zweier ganzer Zahlen ergibt immer eine ganze Zahl
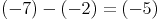
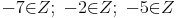
Division:
Der Quotient zweier ganzer Zahlen muss nicht immer eine ganze Zahl ergeben
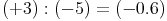
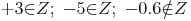
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
Franz Vrabec
Oje! Die erste Zeile (Die Menge der ganzen Zahlen ist die Menge aller positiven und negativen ganzen Zahlen) ist leider falsch! Denn die Null ist auch eine ganze Zahl, gehört aber weder zu den positiven noch zu den negativen ganzen Zahlen!
Admin
Vielen Dank!
Wir haben den Satz bereits umformuliert!
Joce
Subtraktion: Die Differenz zweier ganzer Zahlen ergibt immer eine ganze Zahl
und dann steht da -5 sei kein Element der Ganzen Zahlen Z
Christian Kohout
Vielen Dank! Den Tipp-Fehler haben wir korrigiert. Danke für die Rückmeldungen!
mein Name Ahmed
Ihr habt die Seite gut zusammengesetzt aber Die Erklärungen sind zu Komplex Ich bin nämlich 9 Klässler
Vinc
"Wir haben den Satz bereits umformuliert!"
Habt ihr nicht?!?