Rationale Zahlen
Die Menge der rationalen Zahlen ist die Menge aller positiven und negativen ganzer Zahlen und Zahlen, die als Brüche dargestellt werden können.
Die exakte mathematische Definition lautet:
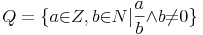
(Die Division durch Null muss ausgeschlossen werden, da dies keine Lösung ergibt)
Rationale Zahlen - Abgeschlossene Operationen
Bei den rationalen Zahlen sind die vier Grundrechnungsarten abgeschlossene Operationen (Die nachfolgenden Beispiele sollen dies veranschaulichen, sind aber keine vollständigen Beweise! Auf diese wurde aus Gründen der Verständlichkeit verzichtet)
Addition:
Die Summe zweier rationaler Zahlen ergibt immer eine rationale Zahl
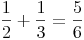
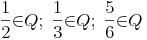
Multiplikation:
Das Produkt zweier rationaler Zahlen ergibt immer eine rationale Zahl
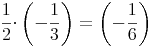
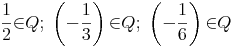
Subtraktion:
Die Differenz zweier rationaler Zahlen ergibt immer eine rationale Zahl
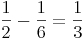
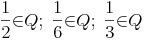
Division:
Der Quotient zweier rationaler Zahlen ergibt immer eine rationale Zahl
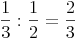
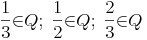
Das Wurzelziehen ist in den rationalen Zahlen nicht abgeschlossen, da die Ergebnisse vieler Wurzeln nicht als Brüche dargestellt werden. Weiters sind auch viele Operationen, die auf Folgen und Reihen aufgebaut sind, nicht abgeschlossen.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
jessica gorgosilich
also ich finde es war nicht so wirklich eine hilfe, weil es auch nicht so gut und genau erklärt worden ist!
Hustensaft
Wieso ist die Addition abgeschlossen?
1/2 + 1/2 = 1 ?