Komplexe Zahl
Da in der Menge der reellen Zahlen die Operation Wurzelziehen nicht abgeschlossen ist (Von negativen Zahlen kann keine Wurzel gebildet werden), gibt es die Menge der komplexen Zahlen.
Man führt dazu eine "besondere Zahl" ein, die folgende Gleichung löst:
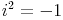
bzw. durch Umformung:
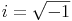
Diese Zahl i wird imaginäre Einheit genannt.
Eine komplexe Zahl setzt sich aus zwei reellen Zahlen (a,b) zusammen, wobei die erste Zahl ein Teil ist, der von der imaginären Einheit i unabhängig ist und die zweite Zahl ein Teil, der von der imaginären Einheit i abhängig ist.
Die komplexe Zahl hat daher folgenden Aufbau:
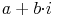
- a ist der Realteil
- b ist der Imaginärteil
Da eine komplexe Zahl ein geordnetes Zahlenpaar aus zwei reellen Zahlen darstellt, können komplexe Zahlen auch nicht mehr auf einem Zahlenstrahl bzw. einer Zahlengeraden abgebildet werden.
Es ist dazu eine Zahlenebene notwendig, die man auch Gaußsche Zahlenebene nennt.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar