Natürliche Zahlen
Für die natürlichen Zahlen gibt es eine ältere und eine neuere Definition. Da man bis in das 13. Jahrhundert nicht mit der Zahl 0 gerechnet hat galt:
Alte Variante:Die Menge der natürlichen Zahlen sind alle positiven, ganzzahligen Zahlen.
N={1,2,3,4,5,6,7, ...}
Man erweiterte die Menge später durch die Zahl 0 und gab diese erweiterte Menge folgendermaßen an:
N0={0,1,2,3,4,5,6,...}
Neue Variante:Nach der neueren Definition ist die Zahl 0 von Haus aus inkludiert. Man sagt:
Die Menge der natürlichen Zahlen sind alle nicht negativen ganzen Zahlen (Somit ist auch die Zahl 0 inkludiert).
N0={0,1,2,3,4,5,6,7,...}
Falls die Menge ohne der Zahl 0 gewünscht ist, schreibt man:
N*={1,2,3,4,5,6,7,...}
Besondere Teilmengen der natürlichen Zahlen
Weiters gibt es einige besonders erwähnenswerte Teilmengen:
Die Menge der natürlichen geraden Zahlen:
NG={0,2,4,6,8,10,12, ...}
Die Menge der natürlichen ungeraden Zahlen:
NU={1,3,5,7,9,11,13, ...}
Die Menge der Primzahlen (alle Zahlen größer 1, die nur durch sich selbst und 1 teilbar sind):
P={2,3,5,7,11,13,17,19,23, ...}
Natürliche Zahlen - Abgeschlossene Operationen
Bei den natürlichen Zahlen sind die Addition und die Multiplikation abgeschlossene Operationen (Die nachfolgenden Beispiele sollen dies veranschaulichen, sind aber keine vollständigen Beweise! Auf diese wurde aus Gründen der Verständlichkeit verzichtet)
Addition:
Die Summe zweier natürlicher Zahlen ergibt immer eine natürliche Zahl
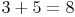
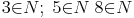
Multiplikation:
Das Produkt zweier natürlicher Zahlen ergibt immer eine natürliche Zahl


Subtraktion:
Die Differenz zweier natürlicher Zahlen muss nicht immer eine natürliche Zahl ergeben
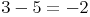
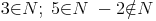
Division:
Der Quotient zweier natürlicher Zahlen muss nicht immer eine natürliche Zahl ergeben
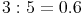
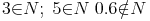
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
mounsef
kann jemand bitte mir die menge der Primzahlen eklären ,
Erich Hnilica, BEd
Liebe(r) Mounsef!
Dazu gibt es einie eigene Seite.
Gib dazu einfach den Suchbegriff "Primzahlen" ins Suchfeld ein.
Liebe Grüße
Mathe-Lexikon-Team
Funktioniert das?
Ja, es funktioniert, cool
Trolli
Gibt es eine gerade natürliche Zahl, die nicht Summer zweier Primzahlen ist? DANKE
O. K.
Gibt es eine gerade natürliche Zahl, die nicht Summe zweier Primzahlen ist? --> ja ( " 2 " )
Jürgen
Wann und wer hat die natürliche Zahlenmenge mit der Null erweitert? Ich hatte die natürliche Zahlenmenge in Verbindung mit der Induktion im Kopf, da fängt man auch mit einem 1. Glied an.
Nicht antworten
Ist ein halbes oder so also alle Bruchzahlen auch eine Natürliche Zahl?
Laura
Warum kam der Unterschied zwischen natürlichen Zahlen mit und ohne Null zustande?
Was hat es mit dem DIN-Norm 5473 aufsich?
DANKE für Antwot :-)
Rafi
Wie sind die natürlichen zahlen die größer als 2 sind ? DANKE
alex
wie sind natürliche zahlen als sind 2?
alex
es hat nicht gestimmt