Ableitungsregeln (Formelsammlung)
Hier finden Sie noch einmal eine Zusammenfassung aller hier vorgestellten Ableitungsregeln.
Konstantenregel
Sei f eine differentierbare Funktion und c eine Konstante, so gilt:
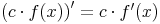
Summenregel
Die Funktionen f und g seien differenzierbar. Es gilt somit:
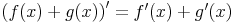
Differenzenregel
Die Funktionen f und g seien differenzierbar. Es gilt somit:
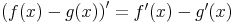
Produktregel
Die Funktionen f und g seien differenzierbar. Es gilt somit:
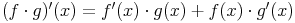
Quotientenregel
Die Funktionen f und g seien differenzierbar. Es gilt somit:
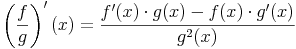
Kettenregel
Ist eine Funktion f1 an der Stelle x0 differenzierbar und eine Funktion f2 an der Stelle f1(x0) differenzierbar, so ist auch die Funktion
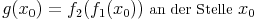
differenzierbar wobei für
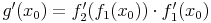
gilt.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar