Differentialrechnung

Konstantenregel

Die Konstantenregel besagt, dass eine Konstante, die aus dem gesamten Funktionsterm herausgehoben werden kann, auch aus einem Differential dieser Funktion herausgehoben werden kann.

Konstantenregel: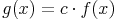

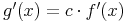
Ist f(x) eine differenzierbare Funktion, c eine reelle Konstante und

$g(x)=c \cdot f(x)$

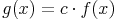
so gilt:

$g'(x)=c \cdot f'(x)$

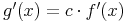
Beispiele zur Konstantenregel

Beispiel 1:

$f(x)=5x^4$

$f'(x)=\left(5x^4\right)'=5 \cdot \left(x^4\right)'=5 \cdot 4x^3=20x^3$

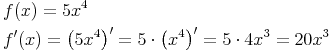
Beispiel 2:

$f(x)=5x^4-15x^3+20x^2$

$f'(x)=\left(5x^4-15x^3+20x^2\right)'=5 \cdot \left(x^4-3x^3+4x^2\right)'$

$f'(x)=5 \cdot \left(4x^3-9x^2+8x\right)$

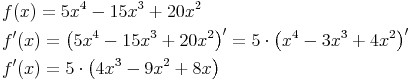
Ein häufig begangener Fehler ist, dass Konstanten herausgehoben werden, die nicht mit der gesamten Funktion multipliziert werden. Ein Beispiel dazu:

$f(x)=3x^2+x$

$f'(x)=\left(3x^2+x\right)'=3 \left(x^2+x\right)'$

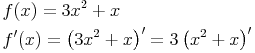
Dieser Umrechnungsschritt ist falsch, da sich der Koeffizient 3 nur auf x² bezieht und nicht auf den gesamten Term!

Dieser Artikel hat mir geholfendas half mir
Dieser Artikel hat mir nicht geholfen... leider nicht
Kommentar zu dieser Seite abgebenKommentar
Frage im Forum stellenForum
Offizielle Facebook-SeiteFacebook

Kommentar schreiben

Kommentare zu diesem Thema