Produktregel

Beim Multiplizieren von Funktionen ist der Sachverhalt nicht mehr ganz so einfach wie bei der Addition und Subtraktion. Mit Hilfe der Produktregel sollte es möglich sein die Ableitung von dem Produkt zweier Funktionen zu finden.

Betrachtet man folgendes Beispiel:

$\begin{align} & f_1(x)=4x^3 \\ & f_2(x)=7x^2 \\ \end{align}$

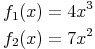
Das Produkt dieser beiden Funktionen ergibt daher:

$(f_1 \cdot f_2)(x) = (4x^3)(7x^2) = 28x^5$

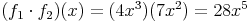
Bildet man nun die Ableitung von den beiden Funktionen f₁ und f₂ und das Produkt dieser beiden

$\begin{align} & f_1'(x)=12x^2 \\ & f_2'(x)=14x \\ & f_1'(x) \cdot f_2'(x)=12x^2 \cdot 14x = 168x^3 \\ \end{align}$

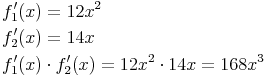
und die Ableitung des Produkts dieser beiden Funktionen:

$(f_1 \cdot f_2)'(x)=\left(28x^5\right)'=140x^4$

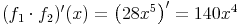
so erkennt man, dass 168x³ und 140x⁴ nicht das selbe Resultat liefern und daher gilt

$f_1'(x) \cdot f_2'(x) \neq (f_1 \cdot f_2)'(x)$

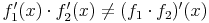
Produktregel

Um die Ableitung des Produkts zweier Funktionen zu lösen, gilt folgende Produktregel:

$(f_1 \cdot f_2)'(x) = f_1'(x) \cdot f_2(x) + f_1(x) \cdot f_2'(x)$

Beispiele zur Produktregel

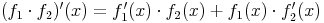
Beispiel 1:

Das erste Beispiel wird nochmals in ausführlichen Schritten erläutert. Natürlich können im Normalfall viel Arbeitsschritte zusammengefasst bzw. in einem Schritt durchgeführt werden.

$f(x) = x^3 \cdot sin(x)$

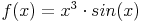
Diese Funktion ist ein Produkt der beiden Funktionen

$f_1(x)=x^3\ \mbox{und}\ f_2(x)=sin(x)$

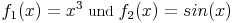
mit den zugehörigen Ableitungen:

$f_1'(x)=3x^2\ \mbox{und}\ f_2'(x)=cos(x)$

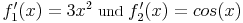
Laut Produktregel gilt nun:

$f'(x)=(f_1 \cdot f_2)'(x) = f_1'(x) \cdot f_2(x) + f_1(x) \cdot f_2'(x)$

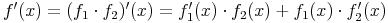
und nach Einsetzen von f₁, f₂, f₁' und f₂':

$f'(x) = 3x^2 \cdot sin(x) + x^3 \cdot cos(x) = x^2 \cdot \left(3sin(x) + x \cdot cos(x)\right)$

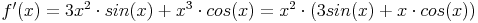
Beispiel 2:

$\begin{align} & f(x) = (2x^3 - 5x) \cdot (2x + 1) \\ & f_1(x) = 2x^3 - 5x\ \mbox{und}\ f_2(x)=2x+1 \\ & f_1'(x) = 6x^2 - 5\ \mbox{und}\ f_2'(x)=2 \\ \end{align}$

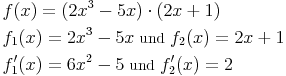
Nach dem Einsetzen erhält man:

$\begin{align} & f'(x) = f_1'(x) \cdot f_2(x) + f_1(x) \cdot f_2'(x) \\ & f'(x) = (6x^2-5) \cdot (2x+1) + (2x^3-5x) \cdot 2 \\ & f'(x) = (12x^3-10x+6x^2-5) + (4x^3-10x) \\ & f'(x) = 12x^3-10x+6x^2-5+4x^3-10x \\ & f'(x) = 16x^3+6x^2-20x-5 \\ \end{align}$

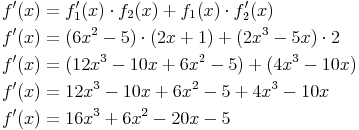
Anmerkung: Natürlich wäre es in diesem Fall möglich (und sinnvoll) gewesen die beiden Binome zuerst zusammenzufassen zu

f(x) = 4x^4+2x^3-10x^2-5x

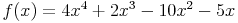
und diese anschließend abzuleiten zu

f'(x) = 16x^3+6x^2-20x-5

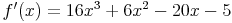
Es sollte hier jedoch ein weiteres Beispiel zur Produktregel gezeigt werden und auch die Allgemeingültigkeit dieser Regel.

Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
3,5
44 Bewertungen

Kommentar #52 von Isabelle Heider 29.11.10 16:36 Isabelle Heider: Weitere Beispiele bzw. Übungsaufgaben wären hilfreich! :)

Produktregel

Produktregel

Produktregel

Kommentar verfassen

Ähnliche Arbeitsblätter