Quotientenregel

Die Quotientenregel ermöglicht das Bilden einer Ableitung vom Quotienten zweier Funktionen

Ähnlich wie bei der Produktregel gilt:

$\frac{f_1'(x)}{f_2'(x)} \neq \left(\frac{f_1}{f_2}\right)'(x)$

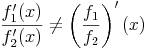
Beispiel:

$f_1(x)=4x^3$

$f_2(x)=8x^2$

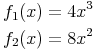
ergeben die Ableitungen:

$f_1'(x)=12x^2$

$f_2'(x)=16x$

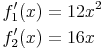
und deren Quotient

$\frac{f_1'(x)}{f_2'(x)}=\frac{12x^2}{16x}=\frac{3x}{4}$

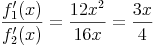
Während

$\left(\frac{f_1}{f_2}\right)'(x)=\left(\frac{4x^3}{8x^2}\right)'=\left(\frac{x}{2}\right)'=\frac{1}{2}$

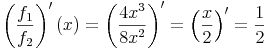
Quotientenregel

Um die Ableitung des Quotienten zweier Funktionen zu lösen, gilt folgende Quotientenregel:

$\left(\frac{f_1}{f_2}\right)'(x) = \frac{f_1'(x) \cdot f_2(x) - f_1(x) \cdot f_2'(x)}{f_2^2(x)}$

Beispiel zur Quotientenregel

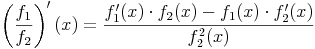
Um diese Regel zu Veranschaulichen, sehen Sie hier die Ableitung des oben angeführten Bruchterms. Auch hier wäre es natürlich möglich, den Bruch zuerst zu vereinfachen und anschließend erst zu differenzieren. Hier soll jedoch gezeigt werden, dass man so zum gleichen Resultat kommt.

$\left(\frac{f_1}{f_2}\right)'(x) = \frac{f_1'(x) \cdot f_2(x) - f_1(x) \cdot f_2'(x)}{f_2^2(x)}$

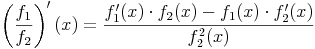
Durch Einsetzen der Teilfunktionen und deren Ableitung erhält man:

$\left(\frac{4x^3}{8x^2}\right)' = \frac{12x^2 \cdot 8x^2 - 4x^3 \cdot 16x}{64x^4}=\frac{96x^4-64x^4}{64x^4}=\frac{32x^4}{64x^4}=\frac{1}{2}$

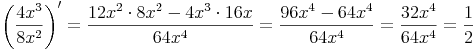
Dieser Artikel hat mir geholfendas half mir
Dieser Artikel hat mir nicht geholfen... leider nicht
Kommentar zu dieser Seite abgebenKommentar
Frage im Forum stellenForum
Offizielle Facebook-SeiteFacebook

Kommentar schreiben

Kommentare zu diesem Thema