Kettenregel
Werden Funktionen verkettet, ist die Kettenregel erforderlich:
Ist eine Funktion f1 an der Stelle x0 differenzierbar und eine Funktion f2 an der Stelle f1(x0) differenzierbar, so ist auch die Funktion
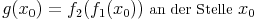
differenzierbar wobei für
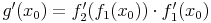
gilt.
Beispiel zur Kettenregel
Das Folgende Beispiel verkettet die beiden Funktionen:
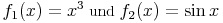
zu
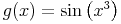
In diesem Fall ist f1 die innere Ableitung und f2 die äußere Ableitung.
Das Resultat lautet somit:
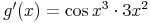
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar