Unter einer Polstelle einer Funktion f(x) versteht man einen Wert x0, wenn ...
- der Wert x0 nicht der Definitionsmenge angehört
- und der Limes der Funktion f(x) gegen x0 ins Unendliche (positiv oder negativ) strebt.
Diese Aussage kann man auch mathematisch kompakt zusammenfassen:
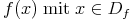 , wenn
, wenn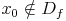 und
und 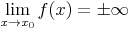 gilt.
gilt.
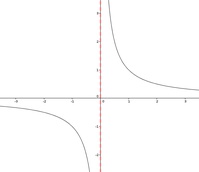
Beispiel: f(x) = 1/x
Diese Funktion hat an der Stelle x = 0 eine Polstelle (in der Abbildung rot strichliert eingezeichnet). Betrachtet man die linke und die rechte Seite unabhängig voneinander, so stellt man fest, dass die linke Seite ins unendlich Positive und die rechte Seite ins unendlich Negative strebt:
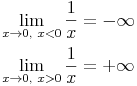
Als Faustregel kann man davon ausgehen, dass Pole vorrangig bei rationalen Funktionen anzutreffen sind. Hierbei muss man lediglich den Nenner auf Nullstellen untersuchen.
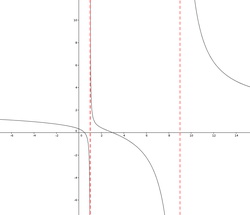
Beispiel 2: Funktion mit zwei Polstellen
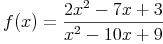
In diesem Fall untersuchen wir den Nenner auf Nullstellen und erhalten:
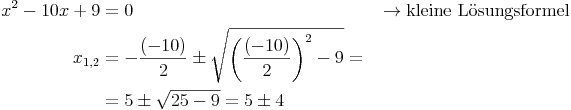
Das bedeutet, dass die Stellen x1 = 1 und x2 = 9 mögliche Polstellen sind.
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar
hb9cti
Einfach erklärt, didaktisch geschickt!