Extremstellen: Hochpunkte, Tiefpunkte und Sattelpunkte

Ermittlung von Extremstellen

Extremstellen stehen in engem Zusammenhang mit dem Monotonie-Verhalten einer Funktion . Wenn eine Funktion in einem Abschnitt streng monoton wächst und im darauf folgenden Abschnitt streng monoton fällt, so muss es am Übergang einen Punkt geben, an dem die Funktion weder steigt noch fällt.

Beispiel: Senkrechter Wurf mit einem Ball

Wirft man einen Ball senkrecht in die Luft, so hat der Ball am Anfang eine hohe Geschwindigkeit und legt daher auch eine längere Strecke zurück (1). Da der Ball durch die Gravitationskraft der Erde verzögert wird, nimmt aber die Geschwindigkeit ab und somit auch der zurückgelegte Weg (2). Irgendwann hat der Ball den höchsten Punkt erreicht (3). Die Geschwindigkeit ist für einen kurzen Moment gleich Null und der Ball legt somit auch keinen Weg zurück. Erst dann ändert sich die Richtung der Bewegung und der Weg den der Ball pro Zeiteinheit zurück legt nimmt wieder zu (diesmal mit umgekehrter Orientierung).

Ballwurf, Wurfhöhe, Beispiel für Maximum

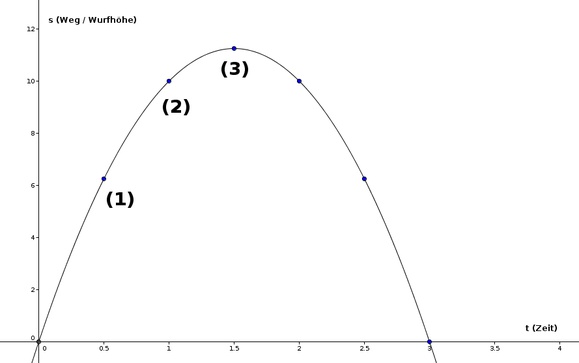In diesem Beispiel wurde angenommen, dass der Ball mit einer Anfangsgeschwindigkeit von 15m/s hochgeworfen wird. Für die Erdbeschleunigung wurde näherungsweise -10m/s² verwendet (statt dem exakten Wert -9.81...)

Die Steigung der Tangente im Weg-Zeit-Diagramm entspricht der Momentangeschwindigkeit zum jeweiligen Zeitpunkt. Hier erkennt man, dass die Steigung der ersten Tangente zum Zeitpunkt t=0.5s (1) sehr hoch ist, zum Zeitpunkt t=1.0s (2) bereits niedriger ist und am höchsten Punkt exakt Null ist.

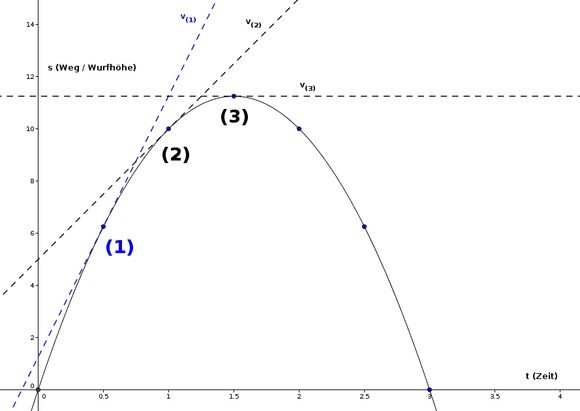Ballwurf, zurückgelegter Weg, mit Tangenten

Die Steigung der Tangenten entsprechen der Geschwindigkeit zum jeweiligen Zeitpunkt

Somit ist ein einfacher Weg gefunden, wie Extremstellen einer Funktion ermittelt werden können:

Extremstellen einer Funktion f(x) ermittelt man, indem man die erste Ableitung f'(x) gleich Null setzt:

f'(x) = 0

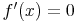
vorausgesetzt, die Funktion f(x) ist zumindest einmal differenzierbar

Welche Arten von Extremstellen gibt es?

Die nachfolgenden drei Abbildungen zeigen drei unterschiedliche Arten von Extremstellen:

Tiefpunkt

Hochpunkt

Scheitelpunkt

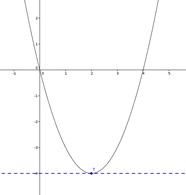
Hochpunkte

sind dadurch charakterisiert, dass der Funktionsabschnitt

vor der Extremstelle streng monoton wächst und
nach der Extremstelle streng monoton fällt.

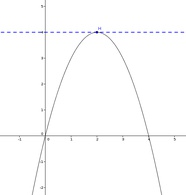
Tiefpunkte

bilden das Gegenstück zu den Hochpunkten, d.h. dass der Funktionsabschnitt

vor der Extremstelle streng monoton fällt und
nach der Extremstelle streng monoton wächst.

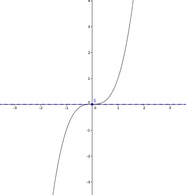
Sattelpunkte

Sattelpunkte stellen einen Sonderfall dar. In diesem Fall ist die Monotonie vor und nach dem Extrempunkt identisch, dennoch erreicht die Kurve kurz einen Punkt, an dem die Steigung der Kurve gleich Null ist (siehe dritte Abbildung).

Um die Art eines Extrempunktes festzustellen, hilft die zweite Ableitung einer Funktion. Hierbei gilt folgender Zusammenhang:

Kennt man eine Extremstelle an der Stelle x, so handelt es sich ...

um einen Hochpunkt, wenn f''(x) < 0 ist
um einen Tiefpunkt, wenn f''(x) > 0 ist
möglicherweise um einen Sattelpunkt, wenn f''(x) = 0 ist

Voraussetzung ist widerum, dass die Funktion zumindest zweimal differenzierbar ist.

Berechnung von Extremstellen

Man geht folgendermaßen vor:

Ermitteln der Extremstellen
Dies erfolgt, indem die erste Ableitung f'(x) mit Null gleichgesetzt wird und die daraus resultierende Gleichung gelöst wird.
Art der Extremstelle ermitteln
Man ermittelt den Funktionswert der zweiten Ableitung f''(x) für jede Extremstelle und prüft nach der o.g. Regel, ob es sich um einen Hochpunkt, Tiefpunkt oder Sattelpunkt handelt (letzterer Fall erfordert etwas genauere Untersuchung).
Den Funktionswert des Extrempunktes ermitteln
Zuletzt fehlt noch der Funktionswert der Extremstelle, damit man auch die genaue Koordinate der Extrempunktes kennt. Hierfür muss lediglich der entsprechende x-Wert der Stelle in die Funktion f(x) selbst eingesetzt werden.

Anmerkung:

Schritt 2 und 3 können auch mehrfach erforderlich sein. Besitzt eine Funktion vier Extremstellen, so müssen Schritt 2 und 3 auch viermal durchgeführt werden.

Beispiele

Wir haben einige Beispiele zusammengestellt, die einige Eigenheiten bei der Ermittlung von Extremstellen aufzeigen. Da dieser Bereich um weitere Beispiele ausgebaut wird, haben wir diese nach Funktionstypen gegliedert in:

Polynomfunktionen

$\begin{align} f(x) & = x^2 + 2x - 1 && \text{Funktion mit einer Extremstelle} \\ f(x) & = x^3 - 12x + 1 && \text{Funktion mit zwei Extremstellen} \\ f(x) & = x^3 && \text{Funktion mit einem Sattelpunkt} \\ f(x) & = x^6 && \text{Sonderfall bgzl. Sattelpunkt} \\ \end{align}$

Die komplette Berechnung der Extremstellen dieser Polynomfunktionen finden Sie hier.

Rationale Funktionen

$\begin{align} f(x) & = \frac{1}{x} \\ f(x) & = \frac{x^2 + x + 1}{1+x^2} \\ \end{align}$

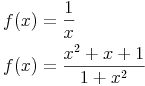
Die komplette Berechnung der Extremstellen dieser rationalen Funktionen finden Sie hier.

Wir werden diesen Bereich um Beispiele mit Logarithmus- und trigonometrischen Funktionen erweitern, die ebenfalls besondere Eigenheiten aufweisen. Weiters richten wir uns gerne auch nach User-Anfragen, hierzu einfach in einem kurzen Kommentar die gewünschte Funktion ergänzen. Wir bitten aber um Verständnis, wenn wir nicht alle Beispiele ausarbeiten, da wir Fälle die ziemlich ähnlich sind nicht wiederholt ausführen möchten (und dies den Rahmen dieser Seite sprengen würde).

Dieser Artikel hat mir geholfen. das half mir
... leider nicht ... leider nicht
Kommentar Kommentar
3,3
176 Bewertungen

Kommentar #9292 von Pixel Puncher 07.10.14 20:27 Pixel Puncher: Die genauere Untersuchung im Falle f"(x)= 0 sollte am besten noch erklärt werden... sonst alles super
Kommentar #44698 von Andreas Matz 09.11.20 17:13 Andreas Matz: Sattelstellen sind KEINE Extremstellen.
Kommentar #45388 von Shukuhi 07.03.21 14:37 Shukuhi: Danke für die Zusammenstellung zum Kapitel Extremstellen.
Nun wollte ich wissen ,warum bei Ermittlung von Sattelpunkt und Wendepunkt f'''(x)ungleich null sein muss?
VG
Kommentar #47593 von Hias1230 27.11.22 18:13 Hias1230: Hi, 2 Tippfehler:

sind dadaurch charakterisiert

Sattelpunkte stellen einen Sonderfall dar. In dieserm

lg aus 1230
Kommentar #47597 von Mathe-Lexikon 28.11.22 11:01 Mathe-Lexikon: Danke @Hias1230, ist ausgebessert!