Um den Definitionsbereich einer Funktion festzulegen ist ein wenig Übung erforderlich. Man muss erkennen, welche Werte nicht eingesetzt werden dürfen. Wir stellen hier die wichtigsten drei Rechenoperationen vor, die eine Einschränkung der Definitionsmenge zur Folge haben:
- Brüche
- Wurzelziehen
- Tangens-Funktion
Definitionsbereich von rationalen Funktionen (Brüche)
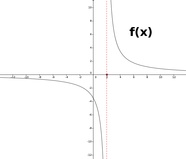
Betrachtet man folgende Funktion
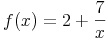
erkennt man, dass prinzipiell jeder Wert eingesetzt werden kann, der Fall x=0 macht allerdings eine Ausnahme. Würde man x=0 einsetzen, so würde dies eine Division durch Null zur Folge haben, die nicht gelöst werden kann. Das bedeutet, dass alle reelle Zahlen außer null erlaubt sind. Man schreibt dies folgendermaßen an:
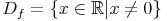
man spricht: "Die Definitionsmenge ist die Menge aller x aus den reellen Zahlen für die gilt: x ist ungleich null.". Eine Weitere Schreibweise ist auch:
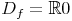
man spricht:
"Die Definitionsmenge ist die Menge der reellen Zahlen, vermindert um 0".
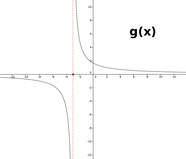
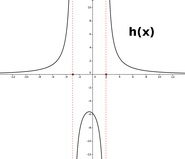
Hier einige weitere Fälle:
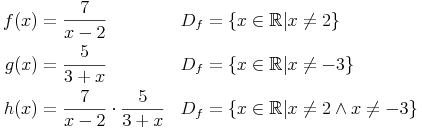
Definitionsbereich von Wurzel-Funktionen
Die Wurzel-Funktion stellt einen weiteren Sonderfall dar. So ist bekannt, dass die Wurzel aus einer negativen Zahl nicht im Zahlenraum der reellen Zahlen lösbar ist. (Hinweis: Im Zahlenraum der komplexen Zahlen ist dies widerum kein Problem)
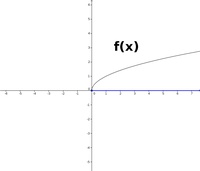
Betrachtet man die folgenden beiden Funktionen,
![\begin{align}
f(x) & = \sqrt{x} \\
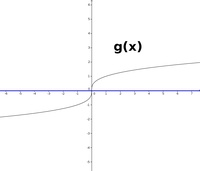
g(x) & = \sqrt[3]{x} \\
\end{align} \begin{align}
f(x) & = \sqrt{x} \\
g(x) & = \sqrt[3]{x} \\
\end{align}](/media/formulas/d4f5906279cd06294167e0aa7dbde4e3.png)
so erkennt man, dass in die Funktion f(x) nur Werte >= 0 eingesetzt werden können. In die Funktion g(x) können widerum alle reelle Zahlen eingesetzt werden, Beispiel:

Daraus ergeben sich folgende Definitionsmengen:
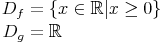
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar