Nullstellen berechnen - eine der ersten Teilaufgaben einer Kurvendiskussion

Eines der ersten Eigenschaften einer Funktion, die man ermitteln kann sind die Nullstellen. Wir erklären hier wie man diese sowohl bei einfachen als auch bei komplexen Aufgaben lösen kann.
Unter Nullstellen versteht man all jene Wertepaare (x, y) einer Funktion f, bei denen der y-Wert null ist. Man erhält die Nullstellen einer Funktion, indem man den Funktionsterm mit null gleichsetzt:

f(x) = 0

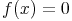
Wie kann man also Nullstellen ermitteln? Fangen wir mit der leichten Variante an:

Grafisches Ermitteln von Nullstellen

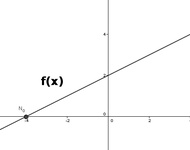
Stellt man den Graph einer Funktion in einem kartesischen Koordinatensystem dar, so erkennt man die Nullstellen, an jenen Stellen an denen der Funktionsgraph die x-Achse schneidet.

Beispiel:
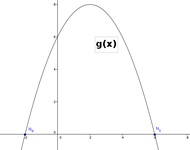
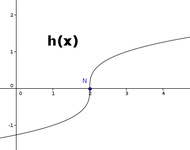
Die nachfolgenden drei Funktionen (f, g, h) besitzen jeweils Nullstellen:

\begin{align} f(x) & = \frac{1}{2} \cdot x + 2 \\ g(x) & = -\frac{1}{2} \cdot x^2 + 2x + 6 \\ h(x) & = \sqrt[3]{x - 2} \\ \end{align}

lineare Funktion, Nullstelle lineare Funktion f(x)
quadratische Funktion mit mehreren Nullstellen Polynom-Funktion g(x)
Wurzelfunktion, Nullstelle Wurzel-Funktion h(x)

Hinweis: Die Abbildungen können vergrößert werden, wenn die eingezeichneten Nullstellen nicht deutlich erkennbar sind. Man sieht anhand der drei Beispiele, dass es Funktionen mit einer oder mehrere Nullstellen gibt. Weiters ist auch leicht nachvollziehbar, dass es auch Funktionen geben kann, die niemals die x-Achse schneiden (oder berühren) und somit auch keine einzige Nullstelle enthalten können. Wir können somit folgendes zusammen fassen:

  • Funktionen können keine, eine oder mehrere Nullstellen besitzen
  • Kennt man den Funktionstyp, kann man die Anzahl der Nullstellen zwar einschränken, allerdings nicht unbedingt festlegen.

Die Darstellung eines Funktionsgraphen in einem Koordinatensystem ist meist dann sinnvoll, wenn man schon über die Charakteristika der jeweiligen Funktion bescheid weiß (und z.B. auch schon die Position der Nullstellen kennt). Kennt man diese noch nicht hat man immer das Problem, dass man nicht weiß welchen Zahlenbereich man darstellen soll. Es könnte auch durchaus sein, dass man einen Abschnitt wählt, in dem keine Nullstellen vorhanden sind, außerhalb dieses Bereichs aber etliche Nullstellen existieren.

Rechnerisches Lösen von Nullstellen

Daher ist es sinnvoller, die Nullstellen zu berechnen. Man geht dabei folgendermaßen vor:

  1. Den Funktionsterm mit 0 gleichsetzen
  2. Die so entstandene Gleichung enthält nur noch eine Variable (meist x benannt)
  3. Die Gleichung nach der Variable lösen
  4. Das Ergebnis entspricht der x-Stelle, an der die Nullstelle auftritt
  5. Der dazu gehörige Punkt wird meist mit großem N und fortlaufendem Index bezeichnet

Im Falle der drei oben angeführten Beispiele, würde dies folgendermaßen aussehen:

Beispiel "f(x)":

\begin{align} f(x) & = 0.5 \cdot x + 2 \\ f(x) & = 0 && \text{

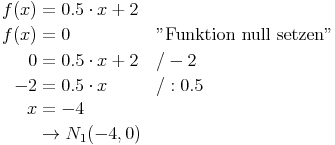
Beispiel "g(x)":

\begin{align} g(x) & = -0.5 \cdot x^2 + 2 \cdot x + 6 && \\ g(x) & = 0 \\ 0 & = -0.5 \cdot x^2 + 2 \cdot x + 6 && / : (-0.5) \\ 0 & = x^2 - 4 \cdot x - 12 && / \text{kleine Lösungsformel} \\ p & = -4 \\ q & = -12 \\ x_{1,2} & = - \frac{p}{2} \pm \sqrt{ \frac{p^2}{4} - q} && \\ x_{1,2} & = - \frac{-4}{2} \pm \sqrt{ \frac{(-4)^2}{4} - (-12)} && \\ x_{1,2} & = + 2 \pm \sqrt{ \frac{16}{4} + 12} && \\ x_{1,2} & = + 2 \pm \sqrt{ 4 + 12} = + 2 \pm \sqrt{16} = +2 \pm 4 && \\ x_1 & = -2\,\ x_2 = 6 \\ & \rightarrow N_1(-2, 0)\,\ N_2(6, 0) \end{align}

Beispiel "h(x)":

\begin{align} h(x) & = \sqrt[3]{x - 2} \\ h(x) & = 0 \\ 0 & = \sqrt[3]{x - 2} && / ^3 \\ 0 & = x - 2 && / +2 \\ x & = 2 \\ & \rightarrow N_1(2, 0) \\ \end{align}

Kommentar verfassen