Wendepunkte sind ein weiteres Merkmal, das Aufschluss über die Charakteristik einer Funktion liefert. Man spricht von einem Wendepunkt an der Stelle x0, wenn sich der Drehsinn einer Funktion vor x0 und nach x0 jeweils unterscheidet. Man erkennt dies daran, dass die Ableitung:
- f'(x) vor x0 monoton steigt und nach x0 monoton fällt oder
- f'(x) vor x0 monoton fällt und nach x0 monoton steigt
Das bedeutet, dass an den Extremstellen der ersten Ableitung Wendepunkte vorliegen können (Dies muss auch - ähnlich wie bei den Extremstellen - durch die nächst höhere Ableitung geprüft werden).
Man erkennt, dass die Vorgehensweise ähnlich ist wie beim Ermitteln der Extremstellen, nur dass die um einen Grad höheren Ableitungen verwendet werden.
Es handelt sich bei w0 dann um einen Wendepunkt, wenn ...
- ... die zweite Ableitung den Funktionswert Null ergibt:
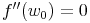
- ... und die dritte Ableitung an dieser Stelle einen Funktionswert ungleich Null ergibt
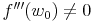
Berechnung der Wendepunkte
Die Schritte sind ähnlich wie beim Berechnen der Extrempunkte :
- Mögliche Wendepunkte ermitteln
Durch Gleichsetzen der zweiten Ableitung f''(x) mit Null erhält man mögliche Wendepunkte - Wendepunkte überprüfen
Die aus Schritt 1 ermittelten Werte müssen anschließend in die dritte Ableitung f'''(x) eingesetzt werden, um zu überprüfen, ob es sich auch tatsächlich um Wendepunkte handelt. Ist das Ergebnis ungleich Null, so handelt es sich um einen Wendepunkt - Funktionswert der Wendepunkte ermitteln
Zuletzt müssen noch die Funktionswerte der bestätigten Wendepunkte ermittelt werden. Dies erfolgt wieder durch das Einsetzen in die Ausgangsfunktion f(x).
Beispiel: Funktion mit zwei Wendepunkten
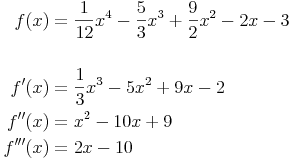
1. Mögliche Wendepunkte ermitteln:
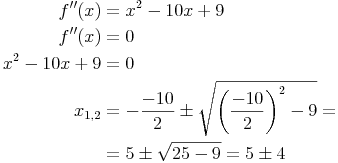
2. Wendepunkte bestätigen:
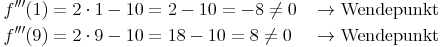
3. Funktionswerte:
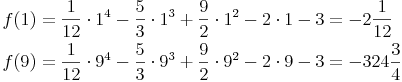
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar