Monotonie einer Funktion feststellen

Mit Hilfe der ersten Ableitung kann festgestellt werden, ob und in welchen Abschnitten eine Funktion (strong) monoton steigend oder fallend ist.

Untersucht man ein Intervall einer differenzierbaren Funktion f, so gelten folgende vier Zusammenhänge: Gilt für alle Werte des Intervalls I ...

  • ... dass f'(x) immer größer 0 ist, dann ist die Funktion streng monoton steigend.
  • ... dass f'(x) immer kleiner 0 ist, dann ist die Funktion streng monoton fallend.

Da die erste Ableitung der Funktion f'(x) bekanntlich die Steigung der Funktion f(x) an der Stelle x liefert, ist nachvollziehbar, dass bei positiver Steigung die Funktionswerte ebenfalls steigen müssen und bei negativer Steigung die Funktionswerte fallen müssen (Falls diese Tatsache noch unklar sein sollte, haben wir dies beim Thema Extremstellen nochmals ausführlicher erläutert).

Beispiel

Von folgender Funktion f(x) soll ermittelt werden, in welchen Intervallen diese Funktion (streng) monoton wachsend oder fallend ist:

f(x) = \frac{2}{3}x^3 - 2x^2 - \frac{2}{3}x + 2

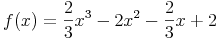
Wir bilden daher zuerst die erste Ableitung f'(x):

\begin{align} f'(x) & = \frac{3 \cdot 2}{3}x^2 - 2 \cdot 2x - \frac{2}{3} \\ f'(x) & = 2x^2 - 4x - \frac{2}{3} \\ \end{align}

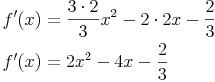
Da wir wissen wollen, in welchem Intervall die Funktion monoton steigend oder fallend ist, ermitteln wir zuerst die Nullstellen der ersten Ableitung. An der Nullstelle der ersten Ableitung f'(x) besitzt die ursprüngliche Funktion f(x) nämlich keine Steigung:

\begin{align} f'(x) & = 2x^2 - 4x - \frac{2}{3} && \text{erste Ableitung mit 0 gleichsetzen} \\ 0 & = 2x^2 - 4x - \frac{2}{3} && \text{für die kleine Lösungsformel umformen} \\ 0 & = x^2 - 2x - \frac{1}{3} && \text{kleine Lösungsformel anwenden} \\ x_{1,2} & = -\frac{p}{2} \pm \sqrt{ \frac{p^2}{4} - q} && \\ x_{1,2} & = -\frac{-2}{2} \pm \sqrt{ \frac{(-2)^2}{4} - (-\frac{1}{3}) } && \\ x_{1,2} & = -1 \pm \sqrt{1 + \frac{1}{3} } && \\ x_{1,2} & = -1 \pm \sqrt{ \frac{4}{3} } = -1 \pm \frac{2}{ \sqrt{3}} && \\ \end{align}

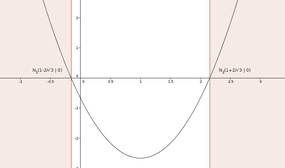
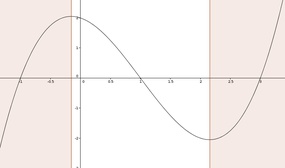
Wir kennen nun die Nullstellen der ersten Ableitung. Betrachten wir nun dazu die beiden Graphen von f(x) und f'(x) und konzentrieren uns insbesondere auf die beiden soeben berechneten x-Werte:

Funktion, Monotonie, erste Ableitung Die Nullstellen der ersten Ableitung unterteilen die Funktion in drei Intervalle
Funktion, Monotonie, erste Ableitung Die ursprüngliche Funktion f(x), die ebenfalls in die gleichen Intervalle unterteilt wird

Bildet man nun diese drei Intervalle

\begin{align} I_1 & ( \infty, && 1 - \frac{2}{ \sqrt{3} } ) \\ I_2 & ( 1 - \frac{2}{ \sqrt{3} }, && 1 - \frac{2}{ \sqrt{3} } ) \\ I_2 & ( 1 - \frac{2}{ \sqrt{3} }, && \infty ) \\ \end{align}

so kann man folgende Eigenschaft feststellen:

Erstes Intervall I1:

  • Die Funktionswerte der ersten Ableitung f'(x) im Intervall I1 sind immer positiv,
  • daher ist die Funktion f(x) streng monoton wachsend.

Zweites Intervall I2:

  • Die Funktionswerte der ersten Ableitung f'(x) im Intervall I2 sind immer negativ,
  • daher ist die Funktion f(x) streng monoton fallend.

Drittes Intervall I3:

  • Die Funktionswerte der ersten Ableitung f'(x) im Intervall I3 sind immer positiv,
  • daher ist die Funktion f(x) wieder streng monoton steigend.
Zusammenfassend kann man folgende Regel aufstellen:

\begin{align} \text{Gilt} &\ f'(x) > 0\ \text{für alle}\ x \in I \rightarrow\ \text{f ist im Intervall I streng monoton wachsend} \\ \text{Gilt} & \ f'(x) < 0\ \text{für alle}\ x \in I \rightarrow\ \text{f ist im Intervall I streng monoton fallend} \\ \end{align}

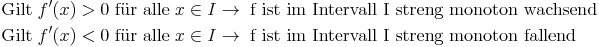
weiters gilt:

\begin{align} \text{Gilt} & \ f'(x) \ge 0\ \text{für alle}\ x \in I \rightarrow\ \text{f ist im Intervall I monoton wachsend} \\ \text{Gilt} & \ f'(x) \le 0\ \text{für alle}\ x \in I \rightarrow\ \text{f ist im Intervall I monoton fallend} \\ \end{align}

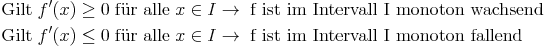
(f(x) ... Funktion, f'(x) ... erste Ableitung, I ... Intervall, dessen Monotonie bestimmt werden soll)
Kommentar #40616 von sabine 10.01.18 23:34
sabine

Leider zu umständlich und von wo weiß ich, dass die Funktionswerte immer positiv/negativ sind?

Kommentar #42904 von effka 19.09.19 11:05
effka

demnach müssten Extrempunkte sowohl als monton steigend als auch als monton fallend gelten?

Kommentar verfassen