Auf dieser Seite stellen wir verschiedene Beispiele von Polynomfunktionen vor und ermitteln jeweils die dazugehörigen Extremstellen. In allen Beispielen bilden wir zu Beginn bereits die erste und zweite Ableitung (wenn möglich) und gehen dann nach der Vorgehensweise vor, die wir in den allgemeinen Erläuterungen zur Berechnung von Extremstellen ausgeführt haben.
Beispiel: Funktion mit einer Extremstelle
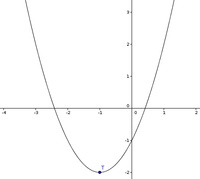
Dies ist eine einfache Polynomfunktion, die eine Extremstelle aufweist.
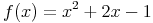
Die dazu gehörigen Ableitungen lauten: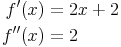
1. Extremwerte ermitteln:
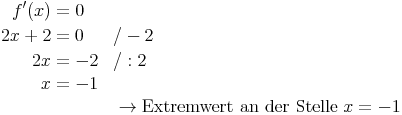
2. Art des Extremwertes ermitteln:

3. Funktionswert des Extrempunktes ermitteln:
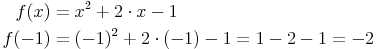
Das bedeutet, diese Funktion besitzt einen Tiefpunkt T1(-1 | -2)
Beispiel: Funktion mit zwei Extremstellen
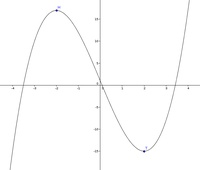
Ein ähnliches Beispiel wie das vorangegangene, jedoch mit dem Unterschied, dass hier zwei Extremstellen behandelt werden müssen:
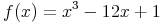
Die dazu gehörigen Ableitungen lauten:
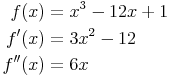
1. Extremstellen ermitteln
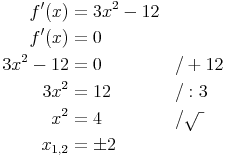
2. Art der Extremstellen ermitteln
Diese Funktion besitzt zwei Extremstellen, einmal bei x1 = -2 und einmal bei x2 = 2. Daher müssen die nächsten beiden Schritte für beide Stellen vorgenommen werden:
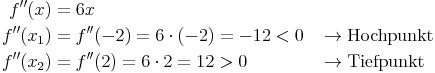
3. Funktionswerte bestimmen
Auch dies muss doppelt durchgeführt werden:
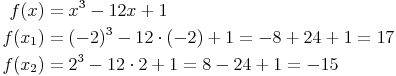
Die ermittelten Extremstellen lauten somit: H(-2|17) und T(2, -15)
Beispiel: Funktion mit einem Sattelpunkt
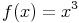
Zu Beginn werden wieder die erste und die zweite Ableitung gebildet:
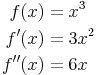
1. Extremstellen ermitteln
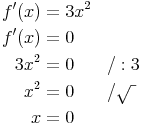
2. Art der Extremstellen ermitteln
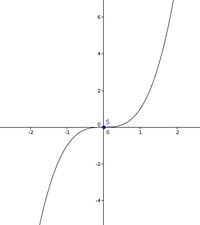
Diese Funktion besitzt möglicherweise einen Sattelpunkt. Der nachfolgende Graph liefert die entsprechende Bestätigung
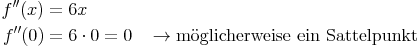
3. Funktionswerte bestimmen
Vom Sattelpunkt wird abschließend noch die Lage des Punktes berechnet:
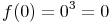
Der Sattelpunkt liegt somit bei S(0|0)
Beispiel: Funktion mit einem Tiefpunkt, obwohl f''(x) = 0 ist
Dieses Beispiel zeigt als Ergänzung zum vorherigen Beispiel mit Sattelpunkt, dass auch Hochpunkte und Tiefpunkte möglich sind, wenn die zweite Ableitung an der entsprechenden Extremstelle als Funktionswert Null liefert.
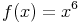
Wir bilden wieder die Ableitungen von f(x):
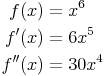
1. Extremstellen ermitteln
![\begin{align}
f'(x) & = 6x^5 \\
f'(x) & = 0 \\
6x^5 & = 0 && / :6 \\
x^5 & = 0 && / \sqrt[5]{\ } \\
x & = 0 \\
\end{align} \begin{align}
f'(x) & = 6x^5 \\
f'(x) & = 0 \\
6x^5 & = 0 && / :6 \\
x^5 & = 0 && / \sqrt[5]{\ } \\
x & = 0 \\
\end{align}](/media/formulas/e4706f64a60e84064125a23d6341e7ed.png)
2. Art der Extremstellen ermitteln
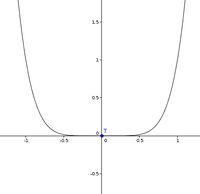
Diese Funktion besitzt möglicherweise einen Sattelpunkt. Der Graph zeigt allerdings, dass es sich hier um einen Tiefpunkt handelt.
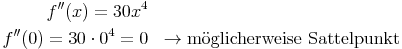
3. Funktionswerte bestimmen
Vom Tiefpunkt wird abschließend noch die Lage des Punktes berechnet:
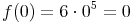
Der Tiefpunkt liegt somit bei T(0|0)
Ermitteln eines Sattelpunktes
In Beispiel 3 und 4 haben wir die Art des Extrempunktes vorweg genommen und mit Hilfe des dazu gehörigen Graphen veranschaulicht. Dies ist allerdings keine praktikable Lösung und es stellt sich die Frage, ob es dafür auch einen rechnerischen Weg gibt.
Folgende Vorgehensweise beschreibt, wie man die Existenz eines Sattelpunktes rein rechnerisch überprüfen kann:
- Extremstelle ermitteln, die möglicherweise ein Sattelpunkt sein könnte,
d.h. f'(x) = 0 und f''(x) = 0 müssen erfüllt sein. - Anschließend werden so lange die Werte der nächsthöheren Ableitungen ermittelt, bis sich ein Wert ungleich Null ergibt.
- Mit folgender Regel kann schließlich die Existenz eines Sattelpunktes festgestellt werden:
- Ist der Grad der Ableitung ungerade, handelt es sich um einen Sattelpunkt
- Ist der Grad der Ableitung gerade, handelt es sich um keinen Sattelpunkt
Dies soll an den beiden vorherigen Beispielen nochmals gezeigt werden:
Beispiel 3:
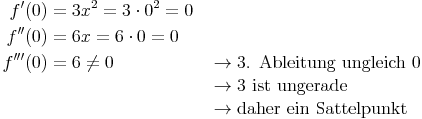
Beispiel 4:

- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar