Dividieren einer positiven ganzen Zahl durch eine negative ganze Zahl
Hier wollen wir Ihnen erklären, wie man eine positive ganze Zahl durch eine negative ganze Zahl dividiert.
Zur einfacheren Erklärung bezeichnen wir positive ganzen Zahlen (also wenn ein + vor der Zahl steht) als Guthaben und negative ganze Zahlen (also wenn ein - vor der Zahl steht) als Schulden.
Multiplikation:Wir leiten die Rechenregel über eine Multiplikation her.
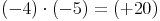
Nun machen wir die Probe dieser Multiplikation.
Probe der Multiplikation:
Bei der Probe der Multiplikation dividiert man das Produkt durch einen Faktor und erhält dadurch den anderen Faktor.
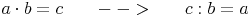
Bei der Probe der Multiplikation dividiert man das Produkt durch einen Faktor und erhält dadurch den anderen Faktor.
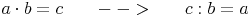
Aus dieser Rechenregel folgt also:
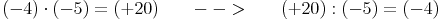
Die Division lautet nun also:
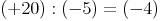
Wir können daraus erkennen, dass man bei der Division einer positiven ganzen Zahl durch eine negative ganze Zahl eine negative ganze Zahl als Ergebnis erhält.
Division einer positiven ganzen Zahl durch eine negative ganze Zahl:
Dividiert man eine positive ganze Zahl durch eine negative ganze Zahl, so ist das Ergebnis (der Quotient) negativ.
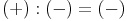
Dividiert man eine positive ganze Zahl durch eine negative ganze Zahl, so ist das Ergebnis (der Quotient) negativ.
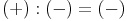
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar