Zusammenfassung Dividieren von ganzen Zahlen
Hier finden Sie eine kurze Zusammenfassung der vorhergehenden Kapitel zum Thema Dividieren mit ganzen Zahlen:
Beispiel 1:
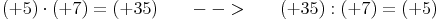
Zusammenfassung: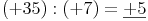
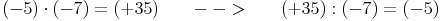
Zusammenfassung: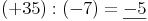
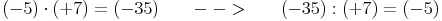
Zusammenfassung: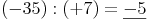
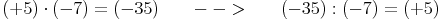
Zusammenfassung: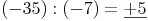
Dividieren von ganzen Zahlen:
Divisionen in der Menge der ganzen Zahlen sind nur möglich, wenn der Dividend ein Vielfaches des Divisors ist.
Haben Dividend und Divisor das gleiche Vorzeichen, so ist der Wert des Quotienten positiv.
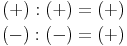
Haben Dividend und Divisor unterschiedliche Vorzeichen, so ist der Wert des Quotienten negativ.
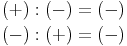
Divisionen in der Menge der ganzen Zahlen sind nur möglich, wenn der Dividend ein Vielfaches des Divisors ist.
Haben Dividend und Divisor das gleiche Vorzeichen, so ist der Wert des Quotienten positiv.

Haben Dividend und Divisor unterschiedliche Vorzeichen, so ist der Wert des Quotienten negativ.
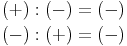
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar