Lösen von Gleichungen durch Umformen (Äquivalenzumformungen)
Kann man bei einfachen Gleichungen die Lösung(en) oftmals durch Ausprobieren herausfinden, so ist dies bei komplizierteren Gleichungen nicht mehr so einfach möglich.
Wie schon erwähnt, kann man sich eine Gleichung als eine Waage im Gleichgewicht vorstellen. Beim Umformen muss darauf geachtet werden, dass dieses Gleichgewicht erhalten bleibt.
Man darf also nur auf beiden Seiten das gleiche wegnehmen oder hinzufügen.
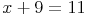
Um herauszufinden, wie groß x ist, ist auf der linken Seite 9 zu viel - deshalb werden 9 weggenommen (was man dann allerdings auf beiden Seiten tun muss)
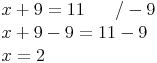
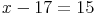
Um herauszufinden, wie groß x ist, ist auf der linken Seite 17 zu wenig - deshalb werden 17 dazugegeben (was man dann allerdings auf beiden Seiten tun muss)
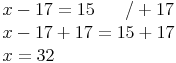
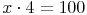
Um herauszufinden, wie groß x ist, ist auf der linken Seite 4 Mal zu viel - deshalb wird durch 4 dividiert (was man dann allerdings auf beiden Seiten tun muss)
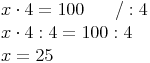
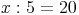
Um herauszufinden, wie groß x ist: Auf der linken Seite ist nur ein Fünftel - deshalb wird mit 5 multipliziert (was man dann allerdings auf beiden Seiten tun muss)
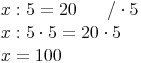
Eine Gleichung bleibt richtig, wenn man auf beiden Seiten der Gleichung dieselbe Zahl addiert / subtrahiert / multipliziert / dividiert.
Um Zahlen von einer Seite "wegzubekommen" muss immer das Gegenteil gemacht werden: Gegenteilig sind addieren - subtrahieren sowie multiplizieren - dividieren
- Dieser Artikel hat mir geholfen. das half mir
- ... leider nicht ... leider nicht
- Kommentar Kommentar